Предмет: Алгебра,
автор: oksana150520
Помогите пожалуйста мне!!!!!!!!!!!!!
Приложения:
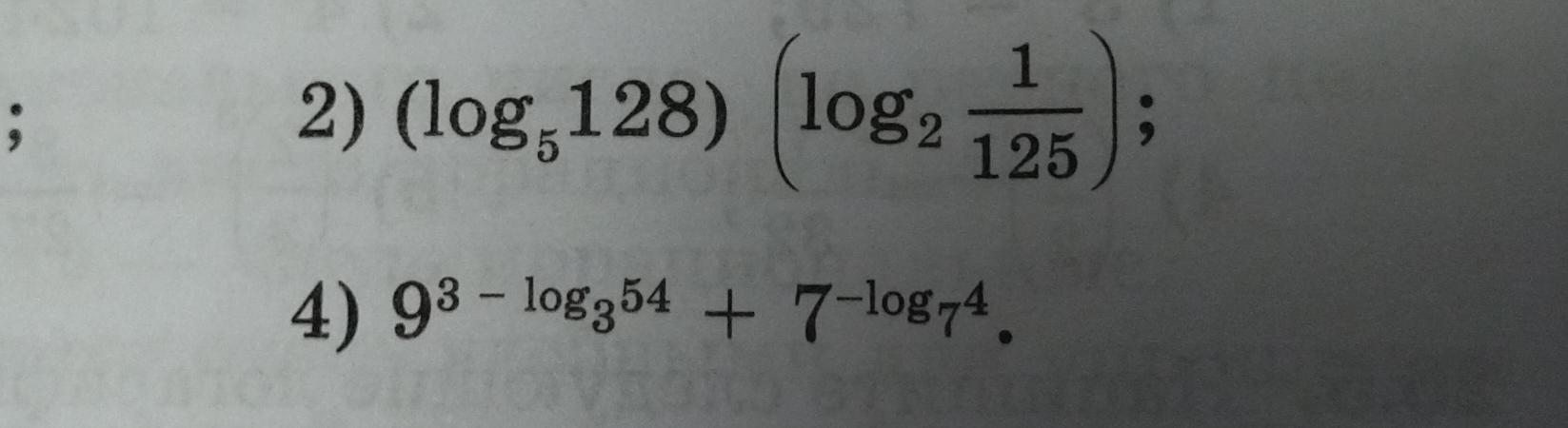
Ответы
Автор ответа:
1
Ответ:
2) ;
4) .
Объяснение:
2) Надо помнить:
Решение:
4) Надо помнить:
Решение:
Похожие вопросы
Предмет: Английский язык,
автор: Юки1253
Предмет: Беларуская мова,
автор: Маргарита678
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: DinkaRou
Предмет: Обществознание,
автор: Fffffol