Question

В равнобедренном треугольнике ABC биссектриса CF равна основанию СВ. Найдите угол CFA.
даю 50 балов

Answer 1

Ответ:

∠CFA = 108°.

Объяснение:

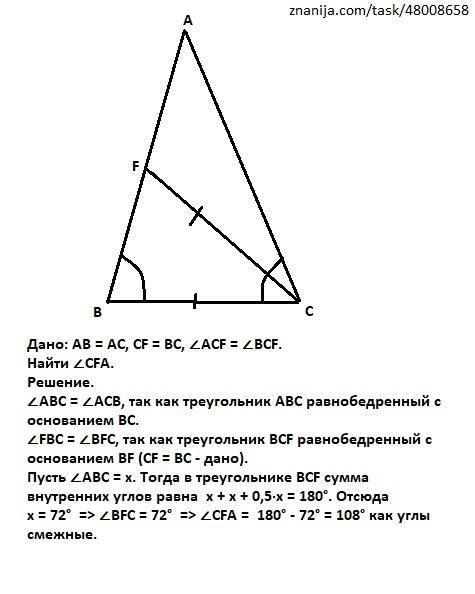
Дано: АВ = AС, СF = BC, ∠ACF = ∠BCF.

Найти ∠CFA.

Решение.

∠АВС = ∠АСВ, так как треугольник АВС равнобедренный с основанием ВС.

∠FВС = ∠BFC, так как треугольник BCF равнобедренный с основанием ВF (CF = BC - дано).

Пусть ∠АВС = х. Тогда в треугольнике ВСF сумма внутренних углов равна  х + х + 0,5·х = 180°. Отсюда

х = 72°  => ∠BFC = 72°  => ∠CFA =  180° - 72° = 108° как углы смежные.