Question

Дана треугольная пирамида все ребра которой равны 5√2. Найти объем пирамиды

Answer 1

Дана треугольная пирамида, все ребра которой равны 5√2. Найти объем пирамиды.

Ответ:

Объем пирамиды равен $41\dfrac{2}{3}$ куб. ед.

Объяснение:

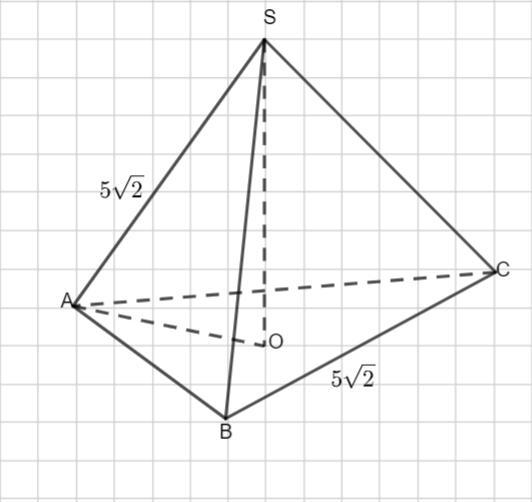
Пусть дана треугольная пирамида ABCS . По условию все ребра равны 5√2.

Объем пирамиды определяется по формуле:

$V= \dfrac{1}{3} \cdot S\cdot H ,$

где S- площадь основания , а  H- высота пирамиды.

Так как все ребра равны, то в основании равносторонний треугольник, площадь которого найдем по формуле:

$S= \dfrac{a^{2}\sqrt{3} }{4} ,$  где а - сторона треугольника.

$S= \dfrac{(5\sqrt{2} )^{2}\sqrt{3} }{4} =\dfrac{50\sqrt{3} }{4} =\dfrac{25\cdot2\cdot \sqrt{3} }{2\cdot2 } =\dfrac{25\sqrt{3} }{2}$  кв. ед.

Так как все боковые ребра тоже равны, то вершина пирамиды проектируется в центр, описанной около треугольника АВС , окружности и

$AO= R ;\\\\R= \dfrac{a}{\sqrt{3} } ;\\\\AO= \dfrac{5\sqrt{2} }{\sqrt{3} } =\dfrac{5\sqrt{2}\cdot\sqrt{3} }{\sqrt{3} \cdot \sqrt{3} }=\dfrac{5\sqrt{6} }{3}$

Рассмотрим Δ AOS - прямоугольный. Применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$SO=\sqrt{AS^{2} -AO^{2} } ;\\SO= \sqrt{(5\sqrt{2} )- \left(\dfrac{5\sqrt{6} }{3}\right)^{2} } =\sqrt{25\cdot2-\dfrac{25\cdot6}{9} } =\sqrt{50-\dfrac{150}{9} } =\sqrt{\dfrac{450-150}{9} } =\\\\=\sqrt{\dfrac{300}{9} } =\sqrt{\dfrac{3\cdot100}{9} } =\dfrac{10\sqrt{3} }{3}$

Тогда найдем объем пирамиды

$V= \dfrac{1}{3} \cdot \dfrac{25\sqrt{3} }{2} \cdot \dfrac{10\sqrt{3} }{3} =\dfrac{25\sqrt{3}\cdot 10\sqrt{3} }{3\cdot2\cdot3} =\dfrac{25\cdot2\cdot 5\cdot3 }{3\cdot2\cdot3} =\dfrac{125}{3} =41\dfrac{2}{3}$  куб ед.