Предмет: Математика,
автор: mystanok9
помогите срочно!!!!!
Приложения:
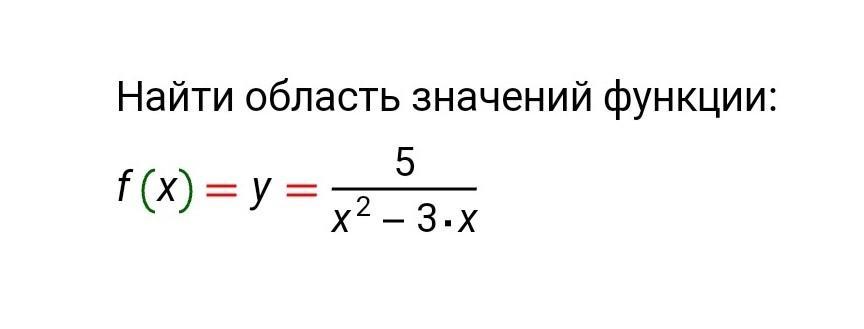
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
найти область значений функции
Ответ: область значений функции:
Похожие вопросы
Предмет: Другие предметы,
автор: klyukva1987
Предмет: Українська мова,
автор: KaPeLa47
Предмет: Русский язык,
автор: Полина200381
Предмет: Русский язык,
автор: nunu33
Предмет: География,
автор: alixalixxD