Предмет: Алгебра,
автор: bb573878
решите неравенство подробно
Приложения:
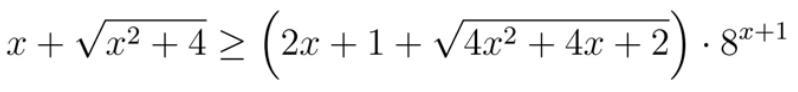
Ответы
Автор ответа:
2
Ответ:
(см. объяснение)
Объяснение:
Выполним деление обеих частей неравенства на 2:
Немного преобразуем полученное:
Выполним умножение обеих частей неравенства на (⇒ знак сохраняем):
Замечаем, что обе части неравенства имеют общий вид и записываем:
Эта функция монотонно возрастает.
Тогда верно, что:
Решение этого неравенства очевидно:
Запишем теперь ответ в виде промежутка:
Неравенство решено!
Похожие вопросы
Предмет: Русский язык,
автор: madina186
Предмет: Русский язык,
автор: вика2326
Предмет: Английский язык,
автор: anndolbilova
Предмет: Математика,
автор: tzgonikovp7svod
Предмет: Математика,
автор: lenochekgavrikova