Question

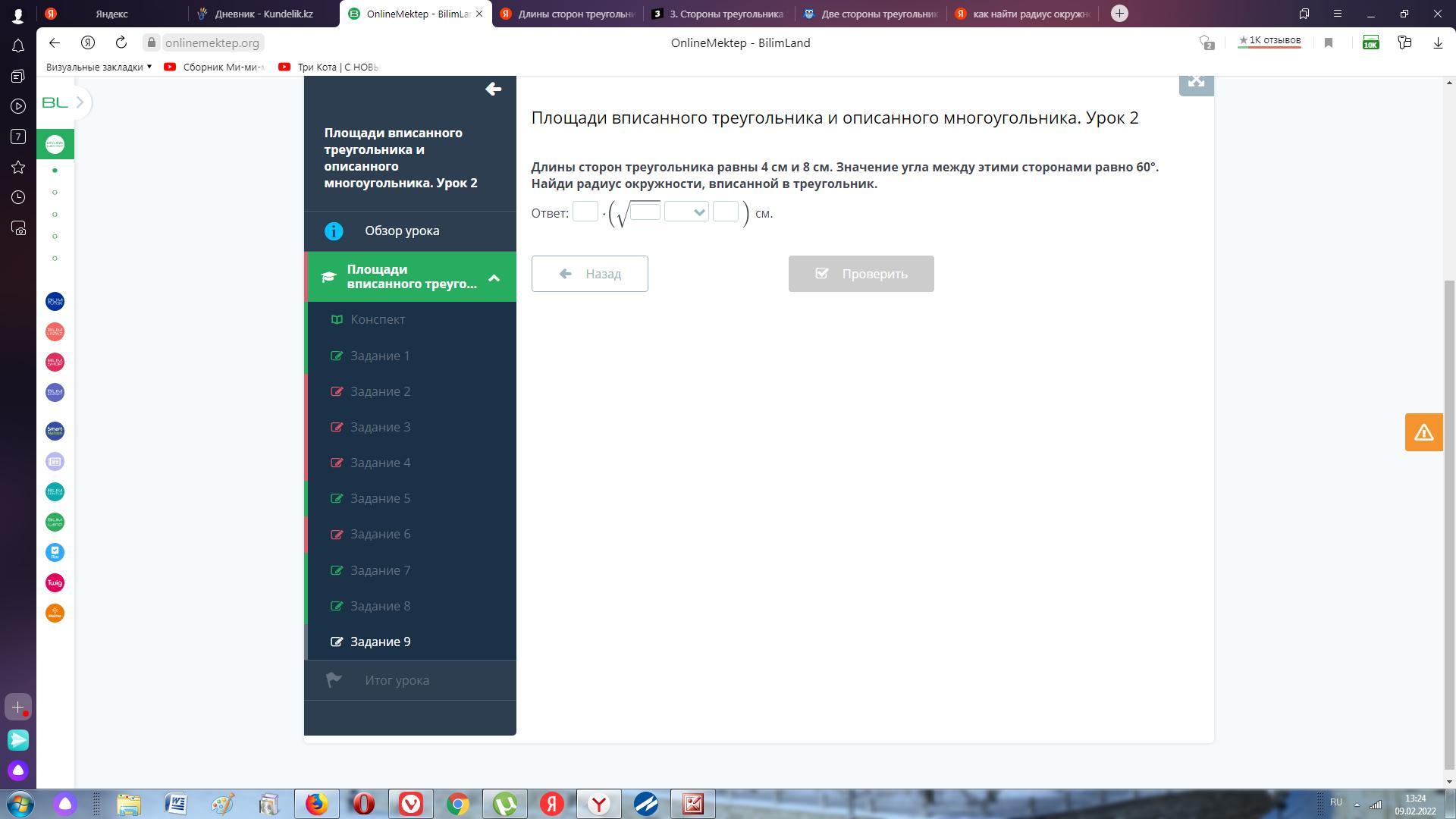
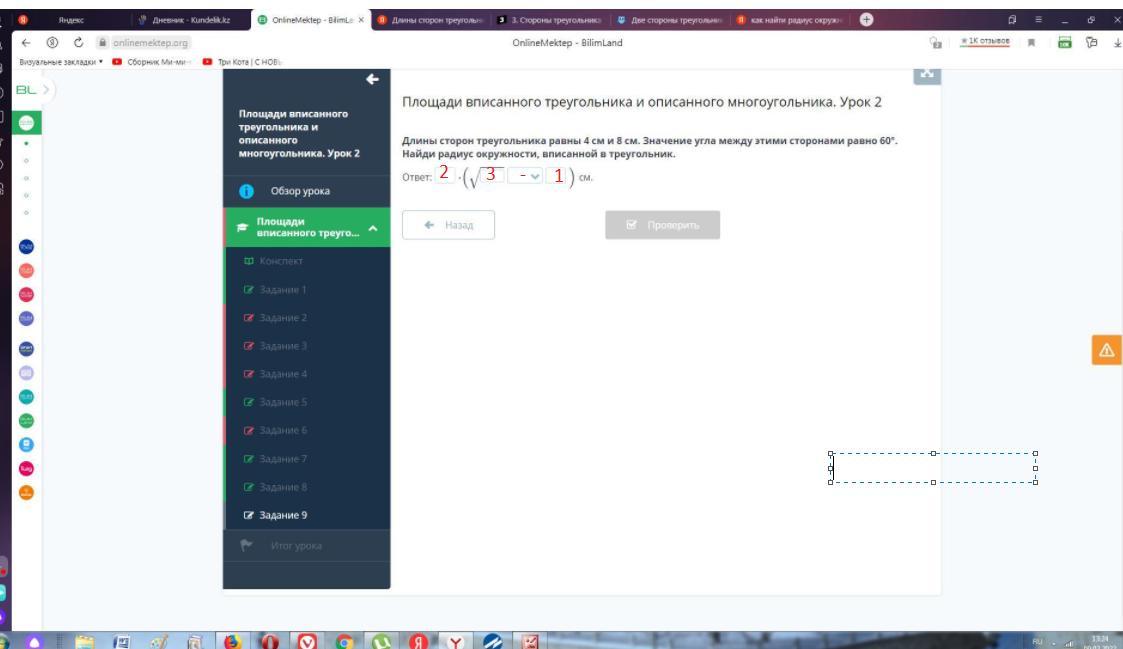
Длины сторон треугольника равны 4 см и 8 см. Значение угла между этими сторонами равно 60°. Найди радиус окружности, вписанной в треугольник.

Answer 1

Ответ:

Радиус окружности, вписанной в треугольник  $2(\sqrt{3} -1)$ см

Объяснение:

Пусть дан треугольник Δ АВС . АВ= 4 см, АС = 8 см, ∠ А =60°.

Найдем сторону ВС по теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

$BC^{2} =AB^{2} +AC^{2} -2\cdotAB\cdot AC\cdot cos A;\\BC^{2} =4^{2} +8^{2} -2\cdot4\cdot 8\cdot cos 60^{0};\\BC^{2}= 16+64-2\cdot32\cdot \dfrac{1}{2} ;\\BC^{2} =16+64-32;\\BC^{2} =48 ;\\BC= \sqrt{48} =4\sqrt{3}$

BC=4√3 см.

Найдем площадь треугольника по формуле

$S= \dfrac{1}{2} \cdot AB \cdot AC\cdot sin A\\S= \dfrac{1}{2} \cdot 4 \cdot 8\cdot sin 60^{0} =\dfrac{1}{2} \cdot 4 \cdot 8\cdot\dfrac{\sqrt{3} }{2} =8\sqrt{3}$

Площадь треугольника Δ АВС равна 8√3 см².

Найдем радиус окружности вписанной в треугольник, по формуле

$r= \dfrac{2S}{P} ,$

где S- площадь треугольника,  P- периметр

$P= 4+8+4\sqrt{3} =12+4\sqrt{3}$

$r= \dfrac{2\cdot 8\sqrt{3} }{12+4\sqrt{3} } ;\\\\r= \dfrac{16\sqrt{3} }{4(3+\sqrt{3}) }; \\\\r= \dfrac{4\sqrt{3} }{3+\sqrt{3} }$

Избавимся от иррациональности в знаменателе.

$r= \dfrac{4\sqrt{3} }{3+\sqrt{3} }=\dfrac{4\sqrt{3}\cdot(3-\sqrt{3} )}{(3+\sqrt{3})(3-\sqrt{3}) }=\dfrac{4\sqrt{3}\cdot(3-\sqrt{3} )}{3^{2} -(\sqrt{3})^{2} }=\dfrac{4\sqrt{3}\cdot(3-\sqrt{3} )}{9-3 }=\\\\=\dfrac{4\sqrt{3}\cdot(3-\sqrt{3} )}{6 }=\dfrac{2\sqrt{3}\cdot(3-\sqrt{3} )}{3 }= \dfrac{6\sqrt{3} -6}{3} =\dfrac{6(\sqrt{3}-1) }{3} =2(\sqrt{3} -1)$

Тогда радиус окружности, вписанной в треугольник равен $2(\sqrt{3} -1)$  см.