Предмет: Математика,
автор: pro201262
Вычислить двойной интеграл, если область интегрирования ограничена следующими линиями, условие на фото
Приложения:
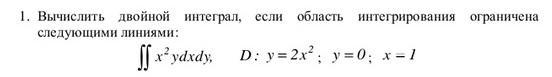
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Прежде всего нам надо расставить пределы интегрирования, чтобы увидеть область интегрирования.
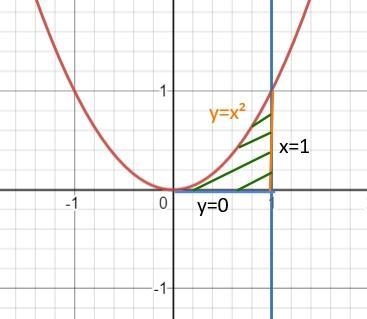
Выполним чертеж.
По чертежу видно, что
0 ≤ у ≤ х²
0 ≤ х ≤ 1
Это мы нашли порядок интегрирования.
Теперь перейдем от двойного интеграла к повторному
Ну, а теперь считаем сначала внутренний интеграл, полагая, что х² константа.
Потом внешний интеграл
Это и есть наш ответ
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: gunayqasimova
Предмет: Русский язык,
автор: kats08
Предмет: Қазақ тiлi,
автор: Zhasminka2004
Предмет: Математика,
автор: NikaRay888
Предмет: Английский язык,
автор: flextboy0067