Предмет: Алгебра,
автор: Pinkiee
Срочно помогите пожалуйста
Приложения:
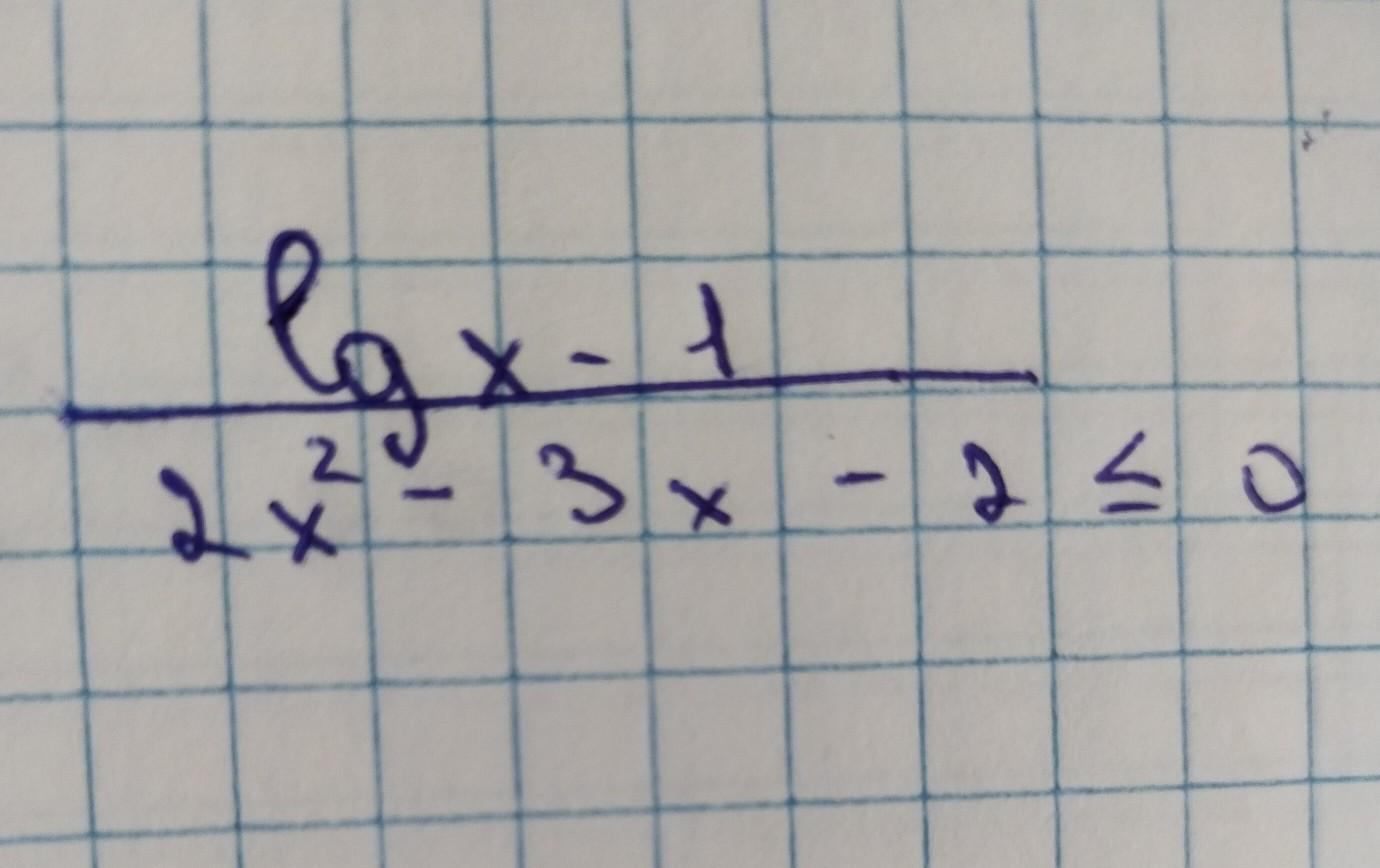
Ответы
Автор ответа:
0
Ответ:
Дробь отрицательна либо равна 0, если числитель неотрицателен, а знаменатель отрицателен, либо наоборот: числитель отрицателен либо равен 0, а знаменатель положителен . Учтём при решении логарифмического неравенства, что функция у=lgx возрастающая .
Пункт b) смотри во вложении, редактор формул перестал работать, невозможно вставить текст .
Приложения:
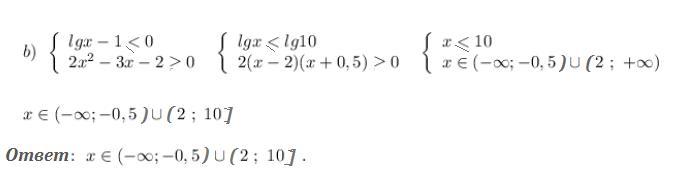
Похожие вопросы
Предмет: Английский язык,
автор: kryuksofya
Предмет: Окружающий мир,
автор: настя4570
Предмет: Русский язык,
автор: бона2005
Предмет: Русский язык,
автор: hdhsvshhs
Предмет: История,
автор: fox201912