Предмет: Геометрия,
автор: alena5566d
ДАЮ 10 БАЛЛОВ, ПОМОГИТЕ ПОЖАЛУЙСТА
Приложения:

Ответы
Автор ответа:
1
Ответ:
Искомый угол ADC равен 90°.
Объяснение:
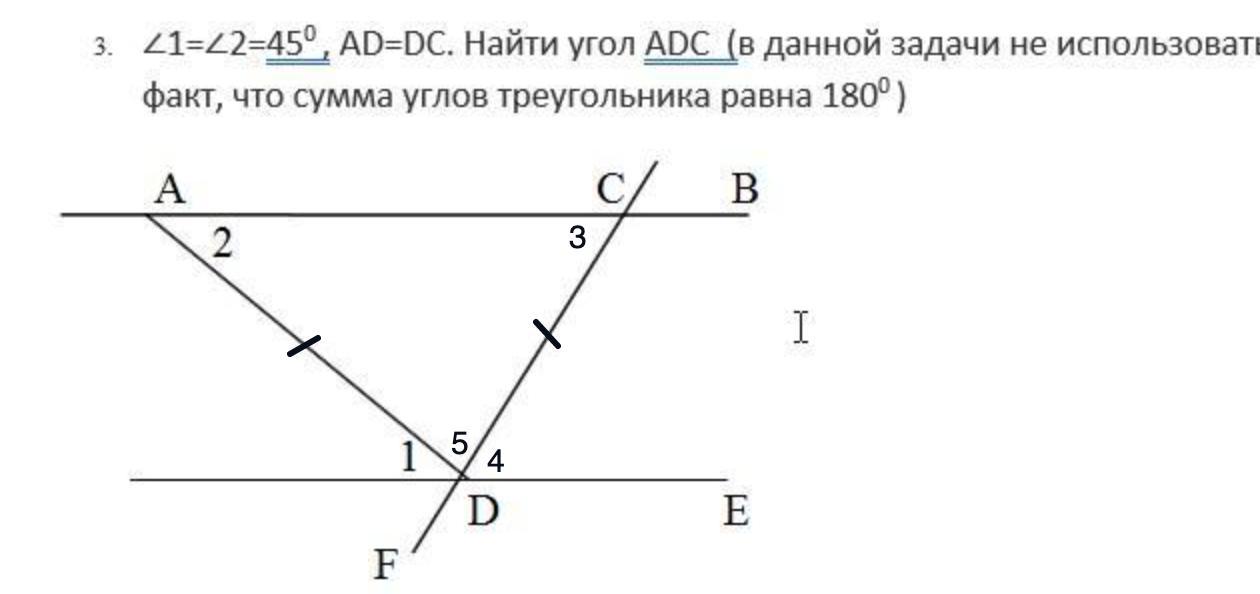
Требуется найти угол ADC.
Дано: АВ и DE - прямые;
AD и DC - секущие;
∠1 = ∠2 = 45°; AD = DC.
Найти: ∠ADC.
Решение:
1. Докажем, что прямые АВ и DE параллельны.
∠1 = ∠2 (условие) - накрест лежащие при АВ и DE и секущей AD.
- Если внутренние накрест лежащие углы равны, то прямые параллельны.
⇒ АВ || DE.
2. Рассмотрим ΔACD.
AD = DC (условие)
- В равнобедренном треугольнике углы при основании равны.
⇒ ∠2 = ∠3 = 45°.
3. ∠3 = ∠4 (накрест лежащие при АВ || DE и секущей CD)
⇒ ∠1 = ∠2 = ∠3 = ∠4 = 45°. (п.1; 2)
4. ∠KDE = 180° - развернутый
или
∠1 + ∠5 +∠4 = 180°
∠5 = 180° - (45° + 45°) = 90°
Угол ADC равен 90°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: владос07
Предмет: Английский язык,
автор: gafuri
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Annamariya9
Предмет: Математика,
автор: almirak92