построить отрезок ab 10 см и разделить точкой C в отношении 3:5 , найти AB:BC AC:AB.
не могу понять как найти AB:BC и AC:AB
СРОЧНО ПОЖАЛУЙСТА

Ответы
Так надо выполнять то, что требуется.
Сначала разделить отрезок АВ на 3+5 = 8 частей.
Длина одной части составит 10/8 = 5/4 или 1,25 см.
Потом определяем длины отрезков:
АС = 3 части, длина АВ = 3*(5/4) = (15/4) или 3,75 см.
СВ = 5 частей, длина СВ = 5*(5/4) = (25/4) или 6,25 см.
Теперь можно отвечать на заданные вопросы.
АВ : ВС = 10/(25/4) = 40/25 = 8/5
АС : АВ = (15/4)/10 = 15/40 = 3/8.
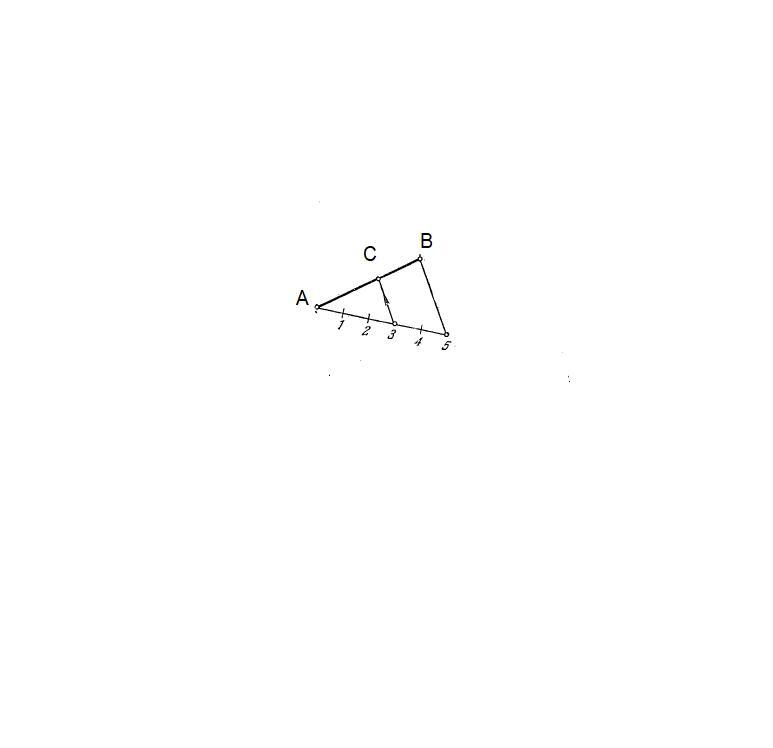
Если задание на теорему Фалеса, то она так звучит:
Деление отрезка прямой на пропорциональные части
Существует теорема Фалеса, которая звучит следующим образом: "если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки".
Используя данную теорему мы можем произвести деление отрезка прямой на пропорциональные части.
Для того чтобы разделить отрезок АВ в соотношении например 3:2 (отсчитывая от точки А), необходимо под произвольным углом из точки А провести вспомогательную прямую. Затем на этой прямой отложить 5 произвольных, но равных между собой отрезков. Далее соединить прямой точки В и 5 и из точки 3 параллельно прямой В5 провести прямую до пересечения ее с отрезком АВ, полученная точка пересечения С разделит отрезок АВ в соотношении 3:2. Мы получим отношение AС:СB = 3:2.