Question

Медиана AM треугольника ABC имеет длину 6 корень из 3.Найдите длину стороны BC, если угол BAC равен 65°, угол BNC равен 115°. N – точка пересечения медиан треугольника ABC.

Answer 1

Ответ:

• BC=12

Объяснение:

• Свойство медиан треугольника: Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины.

1) По свойству медиан треугольника: AN=2NM, откуда AN+NM=AM=$6\sqrt{3}$ ⇔ 2NM+NM=$6\sqrt{3}$ ⇔ 3NM=$6\sqrt{3}$ ⇔ NM=$\bf 2\sqrt{3}$.

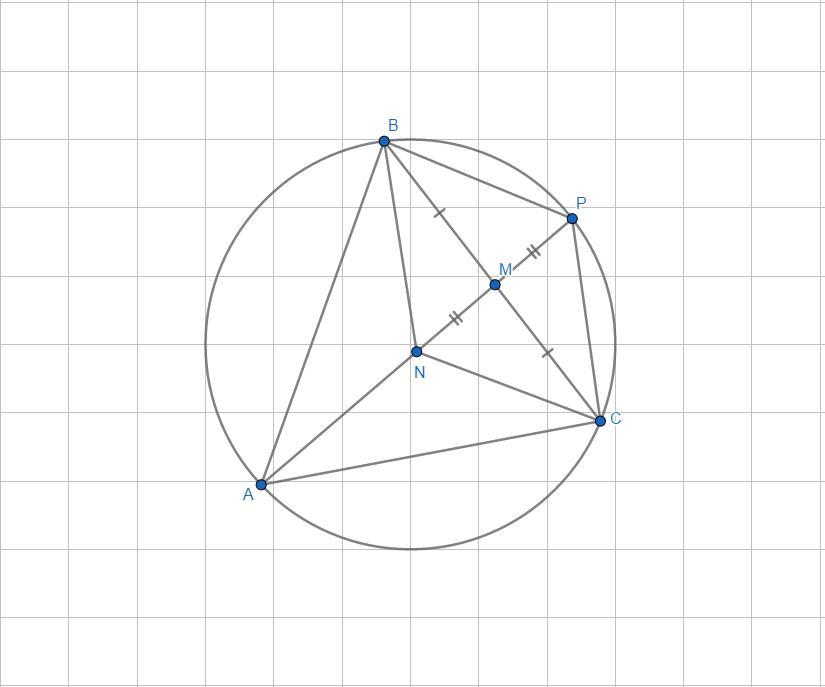
2) Продлим отрезок AM на длину отрезка NM. Получившийся четырёхугольник NBPC - параллелограмм, т.к. BM=MC (т.к. AM - медиана) и NM=MP=$\bf2\sqrt{3}$ (по построению).

Поскольку NBPC - параллелограмм, то ∠BNC=∠BPC=115°.

• Признак вписанного четырёхугольника: Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.

3) Четырёхугольник ABPC - вписанный, т.к. ∠BAC+∠BPC=65°+115°=180°.

Тогда по свойству хорд окружности (пусть BM=MC=x): AM·MP=BM·MC ⇔ $6\sqrt{3} \cdot 2\sqrt{3}$=x·x ⇔ x²=36 ⇔ x=BM=MC=6.

4) BC=BM+MC=6+6=12.