Здравствуйте! Помоги
8+3(5-у^2)(у^2-5)-(у^2-8)^2+(4у^2+2у-1)(у^2-1)+2у
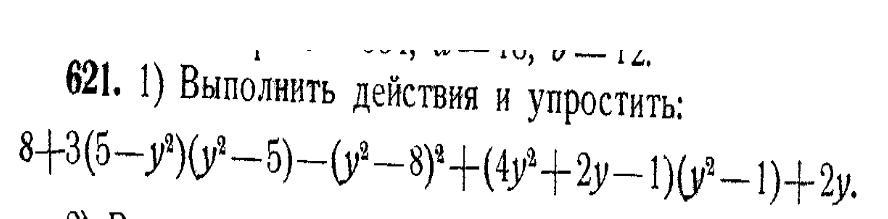
Ответы
Ответ:
8 + 3(5 - y²)(y²- 5) - (y²- 8)² + (4y² + 2y -1)(y² - 1) + 2y =
= 2y³ + 41y² - 130.
Объяснение:
Выполнить действия и упростить выражение.
8 + 3(5 - y²)(y²- 5) - (y²- 8)² + (4y² + 2y -1)(y² - 1) + 2y.
- Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения:
(a-b)²=a²- 2ab + b² .
1) Преобразуем выражение 3(5 - y²)(y²- 5).
Вынесем знак минус за скобки в выражении (5 - y²).
3(5 - y²)(y²- 5) = -3(y² - 5)(y²- 5) = -3(y² - 5)² =
применим формулу квадрата разности двух выражений:
= -3(y² - 5)² = -3(y⁴ - 10y² + 25) =
раскроем скобки с учетом знака минус перед скобками:
= -3y⁴ + 30y² - 75.
2) Преобразуем выражение -(y²- 8)².
Применим формулу квадрата разности двух выражений:
- (y²- 8)² = -(y⁴ + 16y² + 64) =
раскроем скобки с учетом знака минус перед скобками:
= -y⁴ + 16y² - 64
3) Преобразуем выражение (4y² + 2y -1)(y² - 1).
Раскроем скобки, при этом почленно умножим многочлен первых скобок на многочлен вторых скобок.
(4y² + 2y -1)(y² - 1) = 4y⁴ - 4y² + 2y³ - 2y - y² + 1
4) Подведем промежуточный итог.
В результате преобразований получим следующее выражение.
8 + 3(5 - y²)(y²- 5) - (y²- 8)² + (4y² + 2y -1)(y² - 1) + 2y =
= 8 - 3y⁴ + 30y² - 75 - y⁴ + 16y² - 64 + 4y⁴ - 4y² + 2y³ - 2y - y² + 1 +2y.
5) Приведем подобные.
8 - 75 + 64 + 1 = -130;
-3y⁴ - y⁴ + y⁴ = 0;
-2y + 2y = 0.
Тогда получим:
8 - 3y⁴ + 30y² - 75 - y⁴ + 16y² - 64 + 4y⁴ - 4y² + 2y³ - 2y - y² + 1 +2y =
= -130 + 41y² +2y³.
6) Решение в общем виде:
8 + 3(5 - y²)(y²- 5) - (y²- 8)² + (4y² + 2y -1)(y² - 1) + 2y =
=8 - 3(y² - 5)² - (y⁴ + 16y² + 64) + 4y⁴ - 4y² + 2y³ - 2y - y² + 1 + 2y =
= 8 - 3y⁴ + 30y² - 75 - y⁴ + 16y² - 64 + 4y⁴ - 4y² + 2y³ - 2y - y² + 1 +2y =
= 2y³ + 41y² - 130.