Предмет: Алгебра,
автор: helled
решите систему неравенств
Приложения:
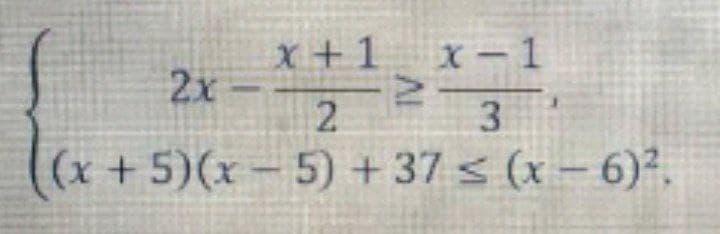
Ответы
Автор ответа:
0
Решение на фотографии
Приложения:
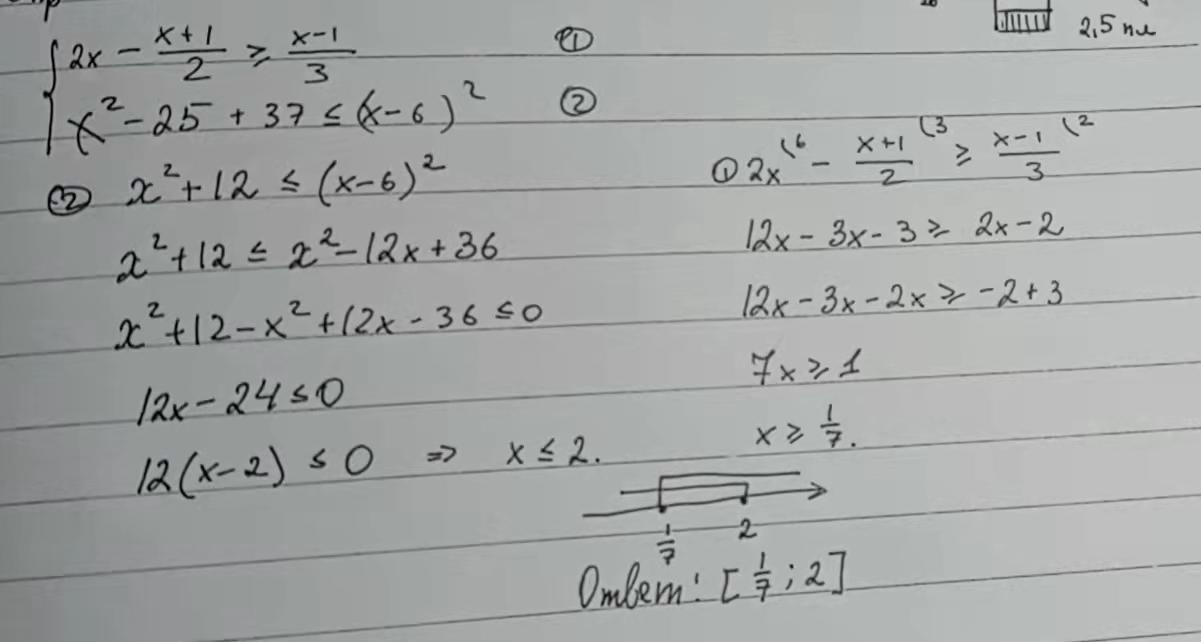
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: Ария1811
Предмет: Русский язык,
автор: dmalvor
Предмет: История,
автор: EEgor98
Предмет: Алгебра,
автор: galinayasinskaya75