Предмет: Алгебра,
автор: dnadyushka2005
1,2,3 очень очень очень очень очень очень срочно, пожалуйста
Приложения:
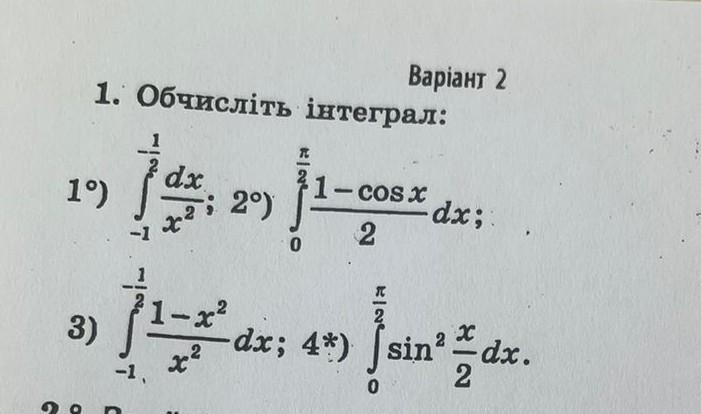
Ответы
Автор ответа:
1
Ответ:
dnadyushka2005:
спасибо большое
Похожие вопросы
Предмет: Немецкий язык,
автор: Maks00p1
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: MisakiOmi
Предмет: Алгебра,
автор: sofico2553