Предмет: Алгебра,
автор: TheLittleMoon
Даю 60 баллов
Найти все углы, образованные при пересечении параллельных прямых
секущей, если разность 2-х односторонних углов равна 86.
TheLittleMoon:
За чертеж накину 50 баллов
Ответы
Автор ответа:
1
Ответ:
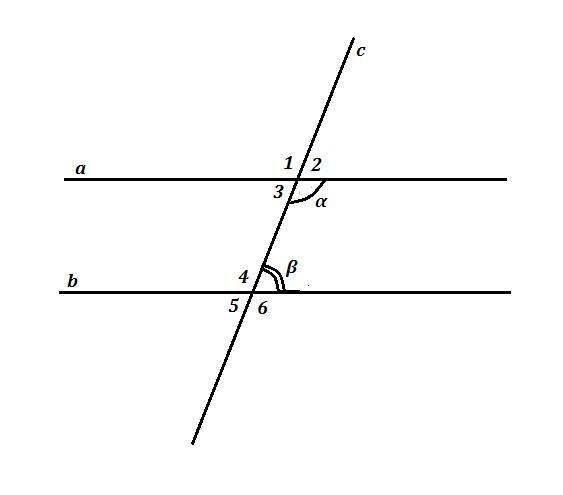
Известно, что сумма внутренних (внешних) односторонних углов, образованных при пересечении параллельных прямых а и b секущей с , равна 180° .
Пусть на чертеже даны внутр. одност. углы α и β , α+β=180° .
По условию α-β=86° .
Эти два условия должны выполняться одновременно, поэтому можно записать систему:
Cложим уравнения системы и вычтем из первого уравнения второе.
Аналогично, можно получить тот же ответ, если брать другие пары односторонних углов .
∠1=∠α=133° как вертикальные углы
∠2+∠α=180° как смежные углы ⇒ ∠2=180°-∠α=180°-133°=47°
∠3= ∠2=47° как вертикальные углы
∠6=∠α=133° как соответственные углы
∠4=∠6=133° как вертикальные углы
∠5=∠β=47° как вертикальные углы
Приложения:
merci <3
Похожие вопросы
Предмет: Русский язык,
автор: kirillzoom1999
Предмет: Русский язык,
автор: kris240515
Предмет: Русский язык,
автор: арина1338
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: kondratenyayanamail