Предмет: Геометрия,
автор: koront2005
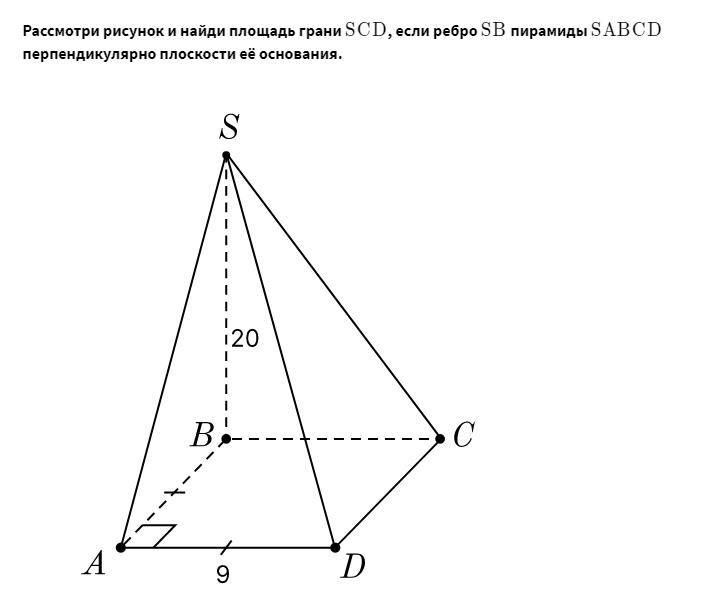
Рассмотри рисунок и найди площадь грани SCD , если ребро SB пирамиды SABCD перпендикулярно плоскости её основания.
Приложения:
Ответы
Автор ответа:
6
Ответ: 9√481/2.
Объяснение:
Основание пирамиды - квадрат АВСD, АВ = ВС = CD = AD = 9.
SB ⊥ (ABCD), значит, SB ⊥ВС и SB ⊥ CD.
ΔSBC - прямоугольный и по теореме Пифагора
SC² = SB² + ВС² = 20² + 9² = 400 + 81 = 481, откуда SC = √481.
По теореме о трех перпендикулярах имеем: SB ⊥ ВС, ВС ⊥ СD, т.е. SВ - перпендикуляр, SC - наклонная, ВС - проекция наклонной, CD - прямая, перпендикулярная проекции наклонной. Значит, SC ⊥ CD, т.е. ΔSCD - прямоугольный, тогда
S(ΔSCD) = 1/2 · SC · CD = 1/2 · √481 · 9 = 9√481/2.
Похожие вопросы
Предмет: Русский язык,
автор: Эльназ111
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: нияз122
Предмет: История,
автор: uskovasasha16
Предмет: Химия,
автор: dfadfasdfa