Question

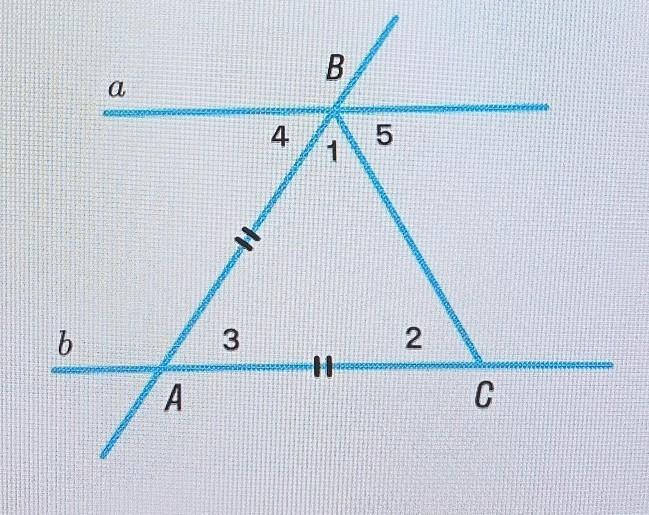
РЕБЯТ ВАЖНО ОЧЕНЬ Реши задачу На рисунке угол 5 = углу 2. Найди градусную меру углов треугольника ABC, если угол 4 в 2,5 раза больше угла 2
​

Answer 1

Ответ:

∠1 = ∠2 = 40°

∠3 = 100°

Объяснение:

Признак параллельности прямых:

• если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

∠5 = ∠2 по условию, а эти углы - внутренние накрест лежащие при пересечении прямых а и b секущей ВС, значит а║b.

Свойство параллельный прямых:

• если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

∠3 = ∠4 как накрест лежащие при пересечении а║b секущей АВ.

АВ = АС по условию, значит ΔАВС равнобедренный с основанием ВС.

∠1 = ∠2 как углы при основании равнобедренного треугольника.

Пусть ∠1 = ∠2 = х, тогда ∠3 = 2,5х.

Сумма углов треугольника равна 180°.

∠1 + ∠2 + ∠3 = 180°

x + x + 2,5x = 180°

4,5x = 180°

x = 40

∠1 = ∠2 = 40°

∠3 = 2,5 · 40° = 100°