Question

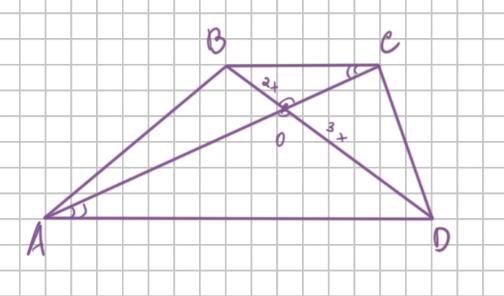
В трапеции АВСD с основаниями АD и ВС диагонали пересекаются в точке О, ВО:ОD =2:3, АС=25см. Найдите АО и ОС.

Мне важно решение, пожалуйста расспишите​

Answer 1

Рассмотрим трапецию ABCD. У данной трапеции ∠BOC = ∠AOD данные углы равны как вертикальные. Так-как это трапеция, то основания трапеции параллельны то есть

BC ∥ AD. Тогда ∠BCA = ∠CAD как накрест лежащие углы при параллельных прямых BC, AD и секущей AC. Рассмотрим △BOC и △AOD, которые являются подобными по 1 признаку (по двум углам). Тогда можем составить отношение сторон:

$\frac{DO}{BO}=\frac{AO}{CO}=\frac{AD}{BC}$.

Так-как по условию AC = 25, то AO = AC - CO = 25 - CO.

BO:OD = 2:3, тогда BO = 2x, OD = 3x Отсюда получаем.

$\frac{3x}{2x}=\frac{25-CO}{CO}$ (Отношение AD/BC нам не понадобится, поэтому его можем убрать).

$\frac{25-CO}{CO}=\frac{3}{2};\\\\2(25-CO)=3CO;\\\\50-2CO=3CO;\\\\50=5CO;\\\\CO=10$

Отсюда: $AO=25-CO=25-10=15$.

Ответ: 15; 10