помогите решить дифференциациальное уравнение
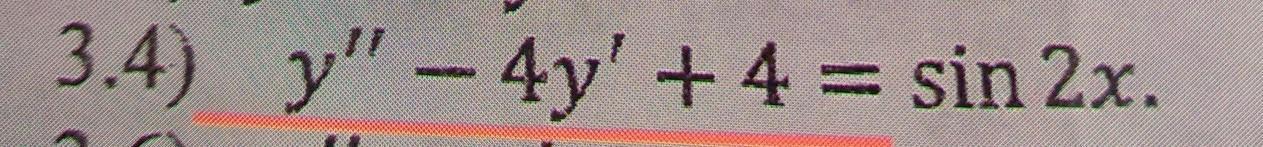
Ответы
Ответ: y=x-1/20*sin(2*x)+1/10*cos(2*x)+1/4*C1*e^(4*x)+C2, где C1 и C2 - произвольные постоянные.
Пошаговое объяснение:
Так как в уравнении отсутствует сама неизвестная функция y, то его порядок можно понизить на 1, то есть до первого. Положим y'=z, тогда y"=z' и уравнение примет вид: z'-4*z+4-sin(2*x)=0. Это - линейное уравнение, для его решения положим z=u*v. Тогда z'=u'*v+u*v' и, подставляя данные выражения в уравнение, мы приходим к уравнению u'*v+u*v'-4*u*v+4-sin(2*x)=0, или v*(u'-4*u)+u*v'+4-sin(2*x)=0. Так как одной из функций u или v мы можем распорядиться произвольно, то поступим так с u и потребуем, чтобы она удовлетворяла уравнению u'-4*u=0. Решая его, находим u=e^(4*x). Подставляя это выражение в уравнение, получаем уравнение e^(4*x)*v'+4-sin(2*x)=0, или v'=dv/dx=e^(-4*x)*sin(2*x)-4*e^(-4*x). Отсюда dv=e^(-4*x)*sin(2*x)*dx-4*e^(-4*x)*dx. Интегрируя, находим v=e^(-4*x)-1/10*e^(-4*x)*cos(2*x)-1/5*e^(-4*x)*sin(2*x)+C1, где C1 - произвольная постоянная. Отсюда z=u*v=1-1/10*cos(2*x)-1/5*sin(2*x)+C1*e^(4*x). И так как z=y'=dy/dx, то dy=z*dx=dx-1/10*cos(2*x)*dx-1/5*sin(2*x)*dx+C1*e^(4*x)*dx. Интегрируя, находим y=x-1/20*sin(2*x)+1/10*cos(2*x)+1/4*C1*e^(4*x)+C2, где C2 - также произвольная постоянная.