помогите с алгеброй!

Ответы
Ответ:
В решении.
Объяснение:
5) Найти координаты точек пересечения графика функции
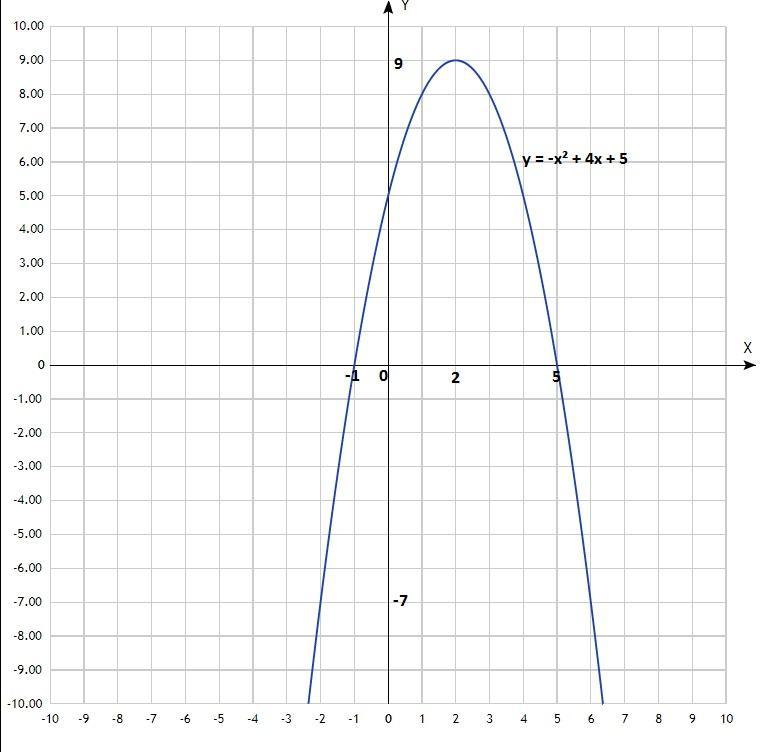
у = -х² + 4х + 5 с осью абсцисс (ось Ох):
Аналитически:
Любой график пересекает ось Ох при у = 0;
-х² + 4х + 5 = 0/-1
х² - 4х - 5 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 16 + 20 = 36 √D=6
х₁=(-b-√D)/2a
х₁=(4-6)/2
х₁= -2/2
х₁= -1;
х₂=(-b+√D)/2a
х₂=(4+6)/2
х₂=10/2
х₂=5;
Парабола пересекает ось Ох в точках: х= -1; х= 5.
Координаты точек пересечения: (-1; 0); (5; 0). б); в);
Графически:
Построить график. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = -х² + 4х + 5;
Таблица:
х -2 -1 0 1 2 3 4 5 6
у -7 0 5 8 9 8 5 0 -7
Согласно графика, координаты точек пересечения параболой оси абсцисс: (-1; 0); (5; 0). б); в);
6) Найти нули функции - точки пересечения параболой
у = х² - 7х + 10 оси Ох.
Аналитически:
Любой график пересекает ось Ох при у = 0;
х² - 7х + 10 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 49 - 40 = 9 √D=3
х₁=(-b-√D)/2a
х₁=(7-3)/2
х₁=4/2
х₁= 2;
х₂=(-b+√D)/2a
х₂=(7+3)/2
х₂=10/2
х₂= 5;
Парабола пересекает ось Ох в точках: х=2; х=5 - нули функции. в);
Графически:
Построить график. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 7х + 10;
Таблица:
х 0 1 2 3 4 5 6 7
у 10 4 0 -2 -2 0 4 10
Согласно графика, х=2; х=5 - нули функции. в);
7) Дана функция у = 2х² - х - 15; найти у(-3).
Подставить в уравнение х = -3 и вычислить у:
у = 2 * (-3)² - (-3) - 15 = 2*9 + 3 - 15 = 6;
у(-3) = 6.
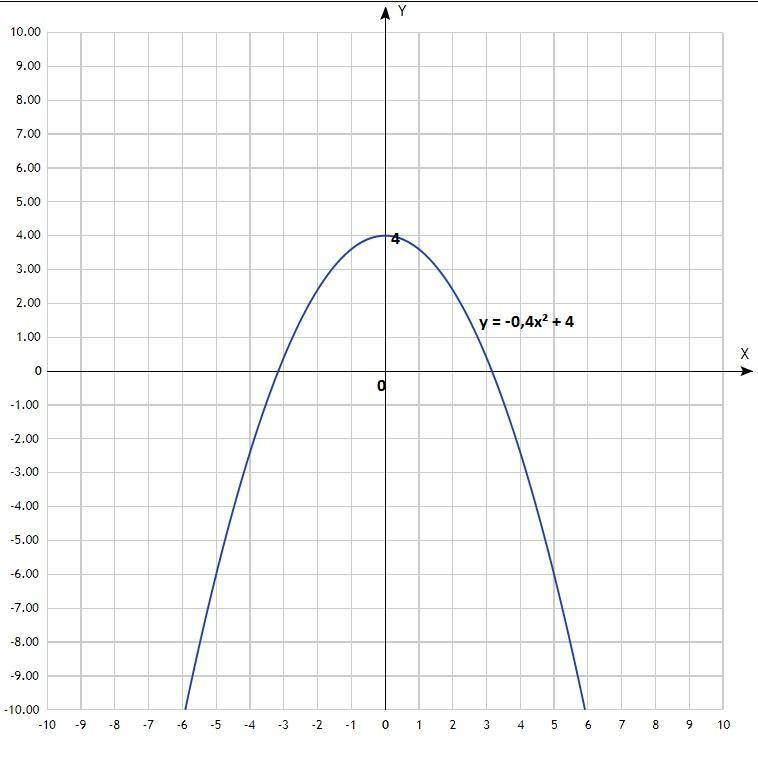
8) Найти ось симметрии графика функции у = -0,4х² + 4.
Ось симметрии Х = х₀;
х₀ = -b/2a;
х₀ = 0/2
х₀ = 0;
Ось симметрии Х = 0. (это ось Оу).
Ось симметрии проходит через точку х=0, ответа такого нет.
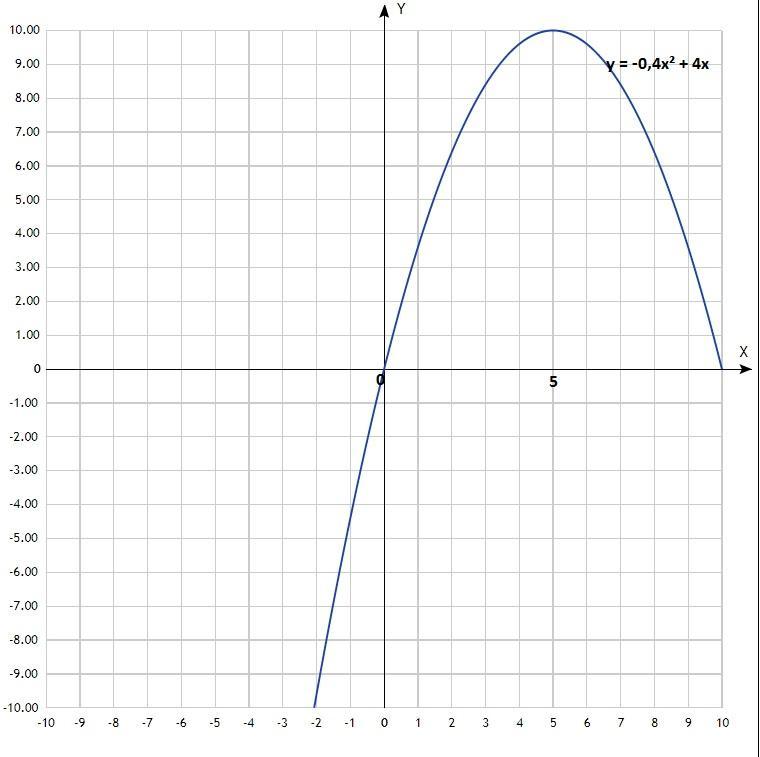
Если уравнение у = -0,4х² + 4х (может, фото обрезано), тогда ответ г) 5.