Предмет: Геометрия,
автор: acexua
Выберите верные утверждения
Высота прямоугольного треугольника равна произведению проекций катетов. Проекция катета равна отношению квадрата этого катета к гипотенузе. Гипотенуза прямоугольного треугольника равна отношению квадрата катета к его проекции на гипотенузу. Высота прямоугольного треугольника равна среднему пропорциональному из проекций катетов на гипотенузу. Высота прямоугольного треугольника равна отношению произведения катетов к гипотенузе. Проекция катета равна отношению квадрата высоты к проекции другого катета.
Ответы
Автор ответа:
5
Ответ:
Верны все утверждения, кроме первого.
Объяснение:
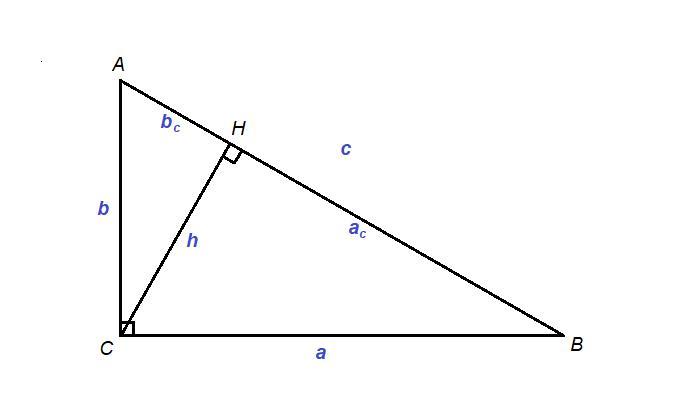
Теорема о среднем пропорциональном в прямоугольном треугольнике:
- высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу:
(1)
- катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:
(2)
Выберем верные утверждения:
- Высота прямоугольного треугольника равна произведению проекций катетов.
Неверно, квадрат высоты равен произведению проекций катетов.
- Проекция катета равна отношению квадрата этого катета к гипотенузе.
Верно. Из равенства (2) получаем:
- Гипотенуза прямоугольного треугольника равна отношению квадрата катета к его проекции на гипотенузу.
Верно. Из равенства (2) получаем:
- Высота прямоугольного треугольника равна среднему пропорциональному из проекций катетов на гипотенузу.
Верно, если считать, что речь идет о высоте, проведенной к гипотенузе, это первая часть теоремы.
- Высота прямоугольного треугольника равна отношению произведения катетов к гипотенузе.
Верно. Эту формулу легко получить из двух формул площади прямоугольного треугольника:
и
- Проекция катета равна отношению квадрата высоты к проекции другого катета.
Верно. Из формулы (1) получаем:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Технология,
автор: OlesyaSavina
Предмет: Українська мова,
автор: jenyamartys
Предмет: Русский язык,
автор: 56qq
Предмет: Экономика,
автор: yuchan53