Предмет: Алгебра,
автор: annaserosh780
Срочно!!!! Даю 60 баллов!!!!
Приложения:
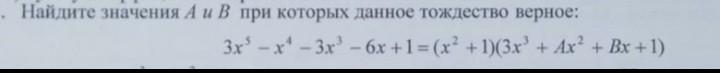
Ответы
Автор ответа:
0
Ответ:
Раскроем скобки в правой части равенства .
Получили равенство двух многочленов. Это возможно лишь тогда, когда равны коэффициенты при одинаковых степенях . Приравняем коэффициенты при одинаковых степенях . Составим систему .
Заданное тождество будет верным при А= -1 и В= -6 .
Похожие вопросы
Предмет: Русский язык,
автор: каприза821
Предмет: Русский язык,
автор: Kseniya3456
Предмет: Немецкий язык,
автор: chachlichknik
Предмет: Математика,
автор: arceniybereza
Предмет: Математика,
автор: White2442