Предмет: Геометрия, автор: FaerVator

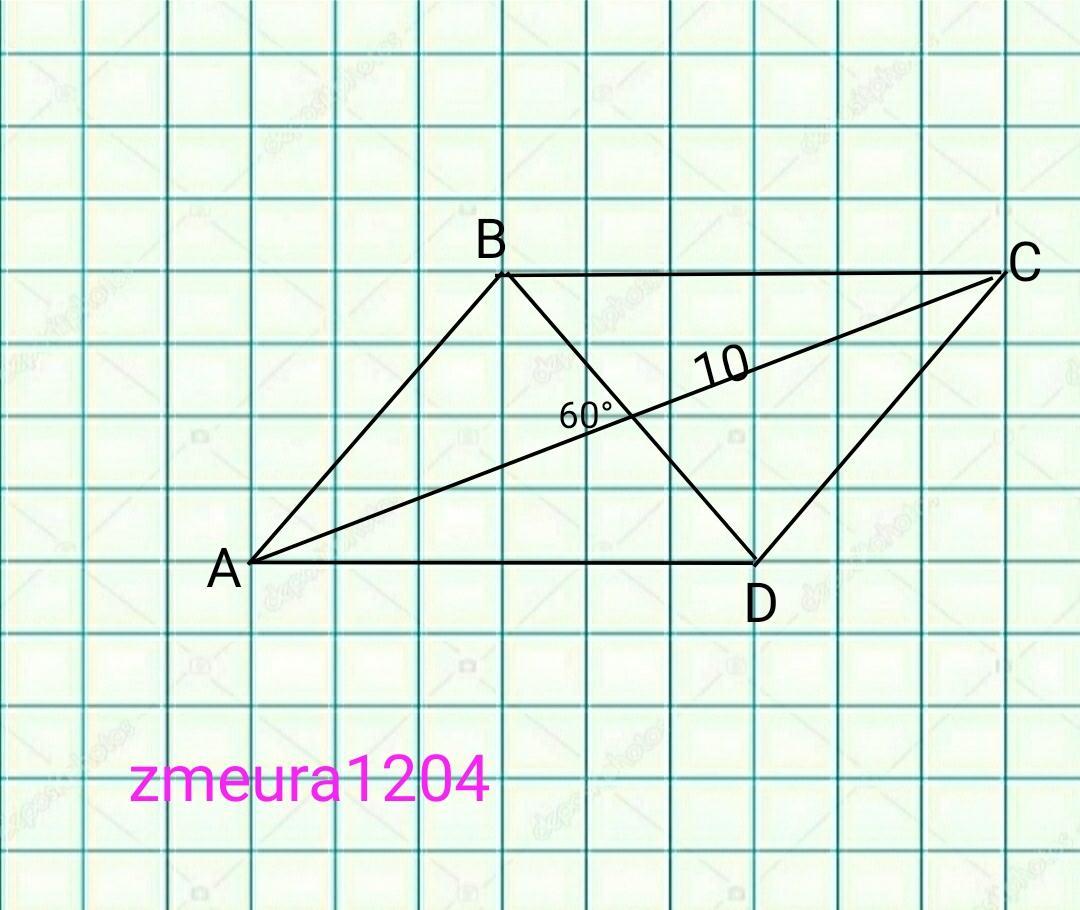
В параллелограмме ABCD диагональ BD равна 10 см, а угол между диагоналями — 60°. Найдите стороны и вторую диагональ параллелограмма, если его площадь равна 30√3 см².

zmeura1204: Диагонали параллелограма точкой пересечения делятся пополам. Дальше теорема косинусов а=√(6²+5²-2*6*5*cos60°) сторона а;

zmeura1204: b=√(6²+5²-2*6*5*cos120°), сторона b.

zmeura1204: Начало: S=1/2*d1*d2*sin60; sin60=√3/2; d1=4*S/d2*√3=4*30√3/10√3=12

zmeura1204: Диагонали параллелограма точкой пересечения делятся пополам. 12:2=6; 10:2=5

zmeura1204: Стороны находим по теореме косинусов. а=√(36+25-30)=√31

zmeura1204: b=√(36+25+30)=√91

FaerVator: и с должен быть 12

zmeura1204: У вас параллелограма откуда с?

FaerVator: ой не с оказывается, просто в конце учебника ответы заглянул там просто написанно 12

FaerVator: спасибо вам большое

Ответы

Автор ответа: zmeura1204

Ответ:
ВD=12см
АВ=√31см
ВС=√91см

Решение:
S=½*AC*BD*sin∠AOC.
sin60°=√3/2
S=½*10*BD*√3/2
BD=4*S/(BD*√3)=4*30√3/10√3=12см.
Диагонали параллелограма точкой пересечения делятся пополам.
АО=АС/2=10/2=5см
ВО=ВD/2=12/2=6см
Теорема косинусов
АВ=√(АО²+ВО²-2*АО*ВО*cos∠AOB)=
=√(5²+6²-2*5*6*1/2)=
=√(25+36-2*5*6*1/2)=√(61-30)=√31см

∠ВОС=180°-60°=120°, смежные углы.
Теорема косинусов.
ВС=√(ВО²+ОС²-2*ВО*ОС*cos∠BOC)=
=√(5²+6²-2*5*6*(-1/2))=√(25+36+30)=
=√91см

Приложения: