Признаки подобия треугольников.
Помогите пожалуйста с заданием по геометрии!
Ответы
Объяснение:
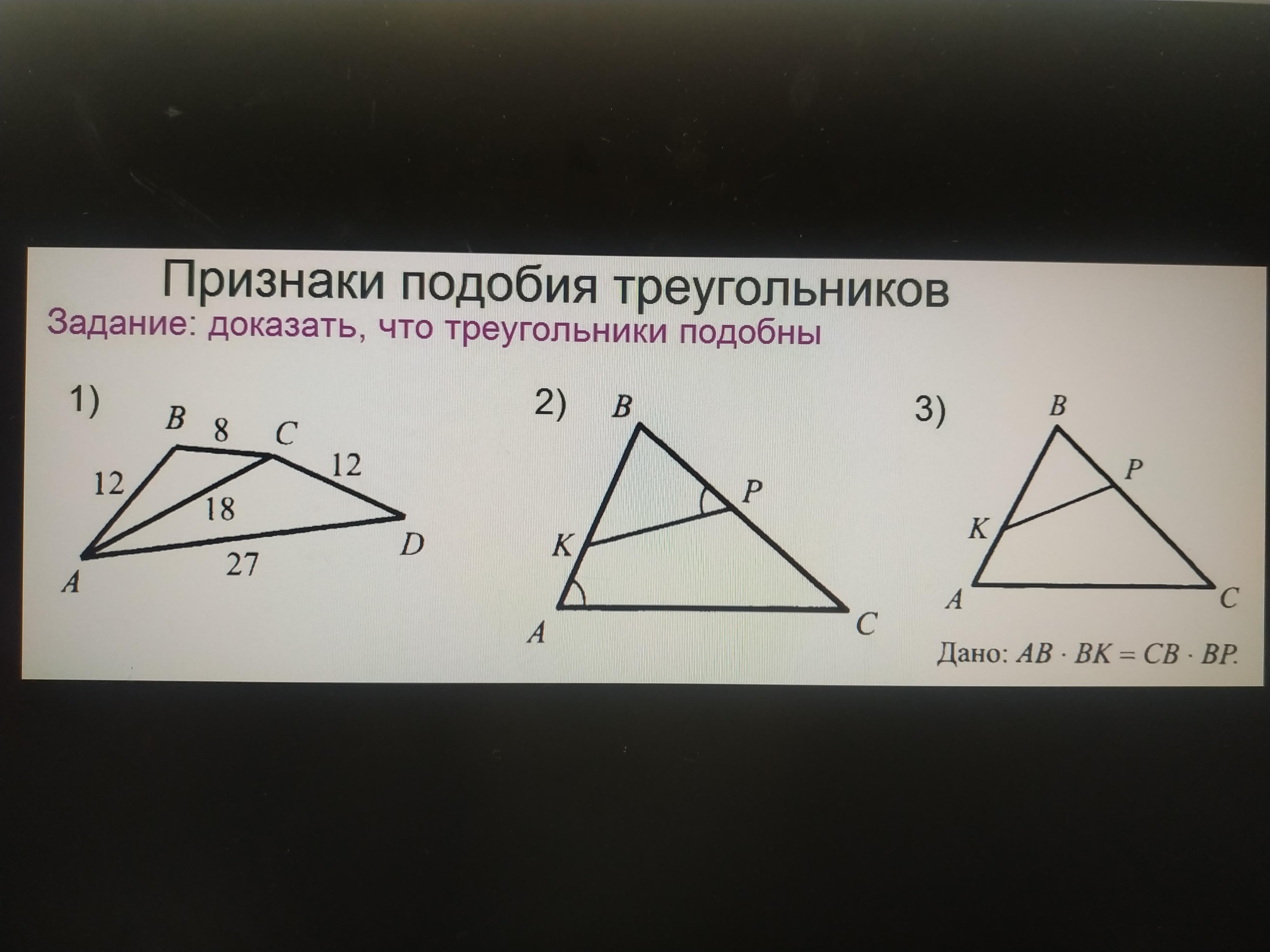
1) Третий признак подобия треугольников: пропорциональны три стороны.
Сопоставим стороны треугольников ABC и ACD:
Меньшая сторона: BC = 8, CD = 12
Средняя сторона: AB = 12, AC = 18
Большая сторона: AC = 18, AD = 27
Все эти три пары относятся друг к другу как 2 к 3
BC / CD = 8 / 12 = 2 / 3
AB / AC = 12 / 18 = 2 / 3
AC / AD = 18 / 27 = 2 / 3
Отсюда следует, что треугольники подобны, что и требовалось доказать.
2) Первый признак подобия треугольников:
Два угла равны
Рассмотрим треугольники KBP и ABC
Угол ABC - общий
Углы KPB и BAC равны по условию
Значит, у этих треугольников соблюдается равенство двух углов, значит, они подобны.
3) Второй признак подобия:
Две стороны треугольников пропорциональны и углы, заключающие эти стороны, равны.
AB * BK = CB * BP
Разделим выражение на CB
(AB / CB) * BK = BP
Разделим выражение на BK
AB / CB = BP / BK
Угол ABC - общий, он заключает пропорциональные стороны треугольников, значит, треугольник ABC подобен треугольнику KBP.