Предмет: Геометрия,
автор: professos
Доказать перпендикулярность прямой и плоскости
Геометрия 10 класс
Срочно!!!!!
Приложения:
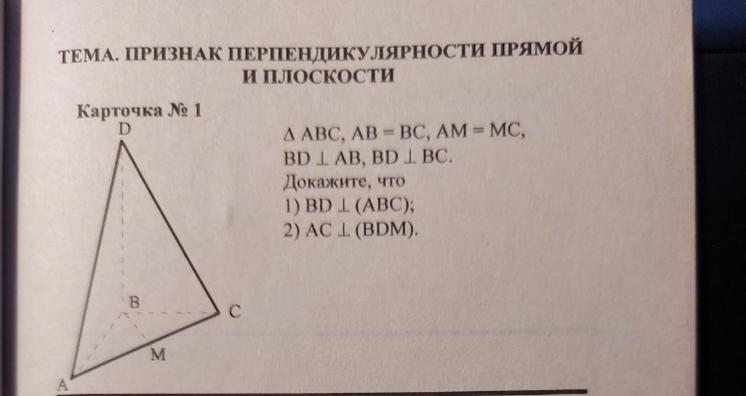
Ответы
Автор ответа:
0
Ответ:
Объяснение:
1) BD⊥AB , BD⊥BC ( BC i AB перетинаються в т. В ) , тому за ознакою перп - сті прямої і площини BD⊥( ABC ).
2) Прямокутний ΔDBC = ΔDBA за двома катетами , бо
АВ = ВС ( за умовою ) і катет BD - спільний . Звідси
AD = CD і , отже , ΔDAC - рівнобедрений . АМ = МС ,
тому DM - медіана , а також висота ΔADC : DM⊥AC .
Але і ВМ⊥АС , бо ΔАВС також рівнобедрений . Таким
чином , AC⊥DM i AC⊥BM , тому за ознакою перп - сті прямої і площини АС⊥(BDM) . ГОТОВО !
Похожие вопросы
Предмет: Другие предметы,
автор: ДаниилРазыков2004
Предмет: Қазақ тiлi,
автор: AlExPlay04
Предмет: Русский язык,
автор: 3умная3
Предмет: Физика,
автор: evomorpheus
2)ΔАВС-равнобедренный и значит медиана ВМ является в нем высотой ВМ⊥АС . Кроме этого ВD ⊥( ABC)⇒BD ⊥ любой прямой этой плоскости.
Получили , что АС⊥ВМ и АС⊥ВD ⇒ по признаку пер.прямой и плоскости АС⊥(ВDM)