Question

Доказать перпендикулярность прямой и плоскости даю 100б

Answer 1

Ответ:

Объяснение:

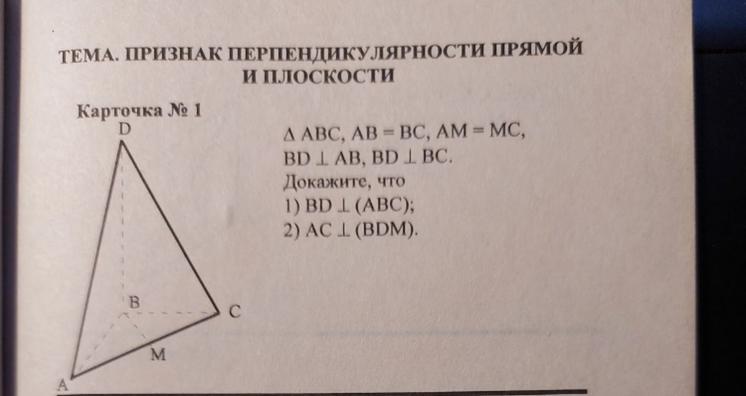
 1) BD⊥AB , BD⊥BC  ( BC  i  AB перетинаються  в т. В ) , тому  за ознакою перп. прямої і площини  BD⊥( ABC ).

2) Прямокутний ΔDBC = ΔDBA за двома катетами , бо

АВ = ВС ( за умовою ) і катет  BD - спільний . Звідси

AD = CD і , отже , ΔDAC - рівнобедрений . АМ = МС ,

 тому DM - медіана , а також висота ΔADC :    DM⊥AC .

 Але і  ВМ⊥АС , бо ΔАВС також рівнобедрений (АВ = ВС) .      Отже, AC⊥DM  i  AC⊥BM , тому  за ознакою

перпендикулярності прямої і площини  АС⊥(BDM) .