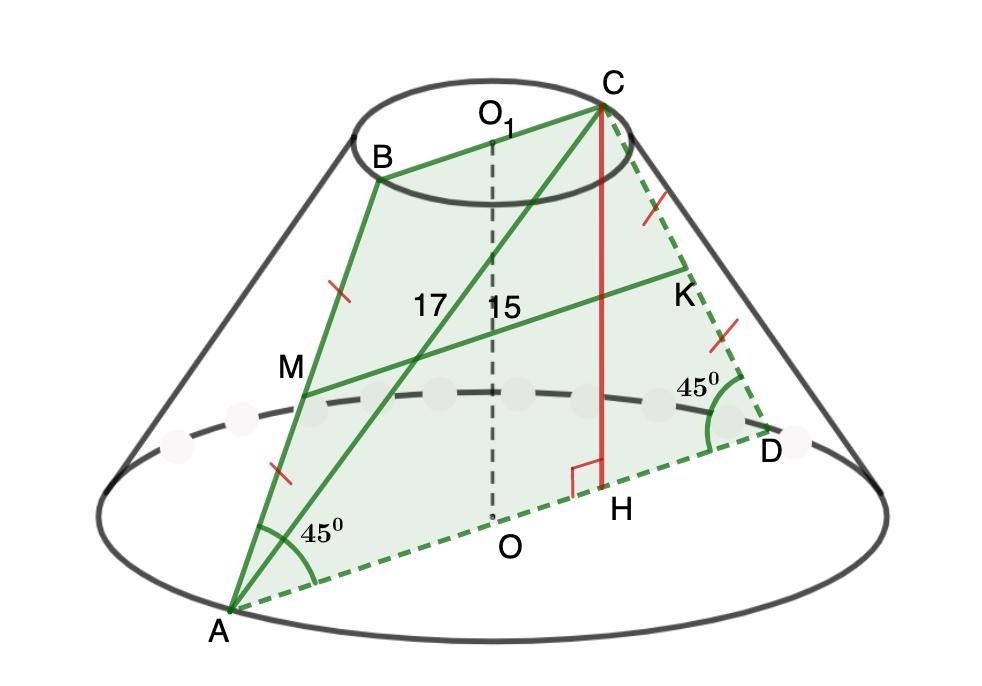
Осевым сечением усечённого конуса является равнобедренная трапеция, у которой острый угол равен 45° , средняя линия - 15 см., диагональ - 17 см.. Найдите площадь боковой поверхности усечённого конуса
Ответы
Ответ:
Площадь боковой поверхности усеченного конуса равна 120√2 π см².
Пошаговое объяснение:
Требуется найти площадь боковой поверхности усечённого конуса.
Дано: Усеченный конус.
ABCD - равнобедренная трапеция, осевое сечение.
∠А = 45°;
МК = 15 см - средняя линия ABCD;
AC = 17 см - диагональ.
Найти: S боковой поверхности усеченного конуса.
Решение:
Проведем высоту CН.
Площадь боковой поверхности найдем по формуле:
S бок = π (r + R) · l ,
где r и R - радиусы оснований, l - образующая.
Нам необходимо найти r, R, и l.
1. Рассмотрим ΔАСН - прямоугольный.
- В равнобедренной трапеции высота, опущенная из вершины тупого угла на большее основание, делит его на части, большая из которых равна полусумме оснований.
Также
- Средняя линия трапеции равна полусумме оснований.
⇒ АН = МК = 15 см.
По теореме Пифагора:
СН² = АС² - АН² = 289 - 225 = 64
СН = √64 = 8 (см)
2. Рассмотрим ΔHCD - прямоугольный.
- В равнобедренной трапеции углы при основании равны.
⇒ ∠А = ∠D = 45°.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠НСD = 90° - 45° = 45°.
- Если в треугольнике два угла равны, этот треугольник равнобедренный.
⇒ ΔHCD - равнобедренный.
СН = HD = 8 см.
По теореме Пифагора:
CD² = HD² + CH² = 64 +64 = 128
CD = √128 = 8√2 (см) - образующая конуса.
3. Большее основание AD равно
AD = AH + HD = 15 + 8 = 23 (см)
Зная среднюю линию МК, найдем меньшее основание ВС:
MK = (BC + AD) : 2
15 = (ВС +23) : 2
30 = ВС + 23
ВС = 7 (см)
4. Найдем площадь боковой поверхности данного усеченного конуса.
ВС - диаметр меньшего основания конуса;
⇒ r = BC : 2 = 7 : 2 = 3,5 (см)
AD - диаметр большего основания конуса;
⇒ R = AD : 2 = 23 : 2 = 11,5 (см)
S бок. = π (3,5 + 11,5) · 8√2 = 120√2 π (см²)
Площадь боковой поверхности усеченного конуса равна 120√2 π см².