Question

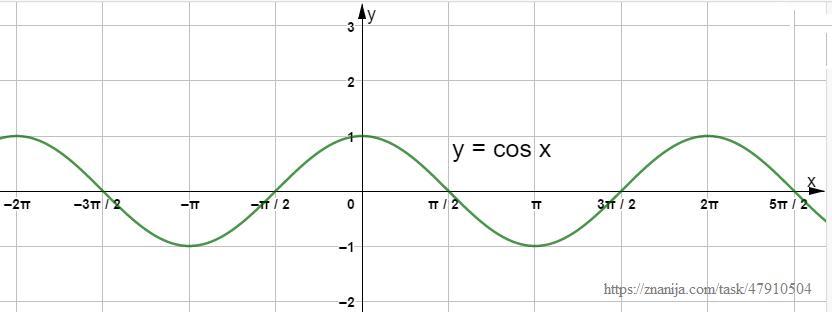
4. Для функции y = cos x найдите: а) область определения; b) область значений; с) наименьший положительный период; d) промежутки убывания; е) промежутки знакопостоянства. f) покажите чётность или нечётность.​

Answer 1

Ответ:

Свойства функции y = cos x. Указать заданные свойства данной функции.

• Областью определения функции называют множество значений аргумента (x), на котором задана функция.

а) Область определения.

Областью определения функции y = cos x является множество всех действительных чисел.

D(y) = R.

• Область значений функции - это множество значений, которые принимает функция на области определения (значения зависимой переменной, y).

b) Область значений.

Областью значений функции y = cos x является множество чисел из промежутка [-1; 1].

• Функция называется периодической, если на области ее определения для каждого значения независимой переменной x выполняется условие:
  f(x - T) = f(x) = f(x + T)     (или f(x) = f(x + nT), n ∈ Z).

с) Наименьший положительный период.

Функция y = cos x периодическая, с наименьшим периодом, равным 2π.

T = 2π.

• Функция возрастает на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, и наоборот, меньшему значению аргумента соответствует меньшее значение функции.

d) Промежутки убывания.

Функция y = cos x убывает на промежутках:

[0 + 2πn; π + 2πn], n ∈ Z.

(Для сведения. промежутки возрастания. Функция y = cos x возрастает на промежутках:

[π + 2πn;  2π + 2πn], n ∈ Z).

• Промежутки знакопостоянства функции, это промежутки значений аргумента, на которых функция сохраняет свой знак (положительна, или отрицательна).

е) Промежутки знакопостоянства.

cos x >0.  Функция y = cos x принимает положительные значения на промежутках:
$\displaystyle \left(-\frac{\pi }{2}+2\pi n ;\;\;\frac{\pi}{2} +2\pi n \right); n \in Z.$

cos x < 0.   Функция y = cos x принимает отрицательные значения на промежутках:
$\displaystyle \left(\frac{\pi }{2}+2\pi n ;\;\;\frac{3\pi}{2} +2\pi n \right); n \in Z.$

• Функция является четной, если f(-x) = f(x);  нечетной, если f(x) = -f(x).
  Если f(-x) ≠ f(x) ≠ -f(x), то четность не определена, функция общего вида.

f) Показать чётность или нечётность.​

Функция y = cos x четная.

cos(-x) = cos x.

Для сведения. Приложим график функции y = cos x.