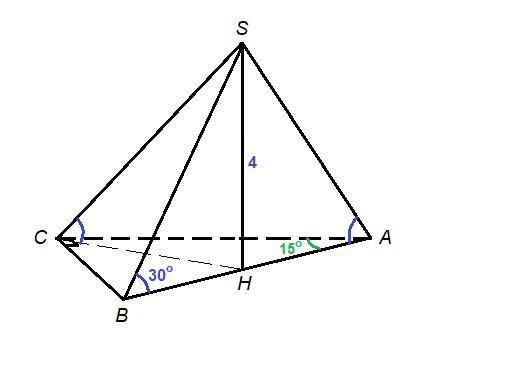
Основанием пирамиды является прямоугольный треугольник с углом 15°, высота пирамиды равна 4 см, а боковые рёбра образуют с плоскостью основания углы 30°. Найдите объём пирамиды.
Ответы
Ответ:
32 см³
Объяснение:
Чтобы найти объем пирамиды, надо знать площадь основания и высоту пирамиды.
Проведем SH - высоту пирамиды. SH = 4 см.
Тогда АН, ВН и СН - проекции наклонных SA, SB и SC на плоскость основания соответственно.
∠SAH = ∠SBH = ∠SCH = 30°, значит прямоугольные треугольники равны ΔSAH = ΔSBH = ΔSCH по катету (SH - общий катет) и противолежащему острому углу. Следовательно
НА = НВ = НС, т.е. Н - это центр окружности, описанной около основания.
- В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
Итак, Н - середина гипотенузы АВ.
ΔSBH: ∠SHB = 90°,
ВН = SH · ctg 30° = 4√3 см
АВ = 2ВН = 2 · 4√3 = 8√3 см
ΔАВС: ΔАСВ = 90°, ∠ВАС = 15°
АС = АВ · cos 15° = 8√3 · cos 15°
BC = AB · sin 15° = 8√3 · sin15°
Площадь основания:
S = 0,5 · AC · BC
S = 0,5 · 8√3 · cos 15° · 8√3 · sin15°
Применим формулу синуса двойного угла:
S = 4 · 3 · 4 · sin 30° = 48 · 0,5 = 24 см²
Объем пирамиды:
см³