Question

.................................

Answer 1

Ответ:

Площадь параллелограмма ABCD равна 78

Объяснение:

Дано:

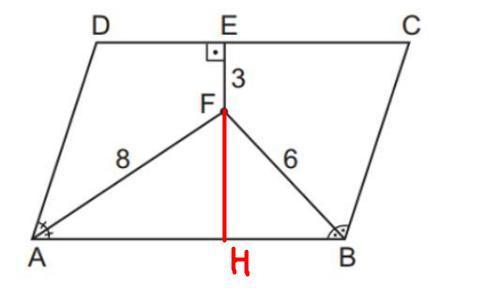
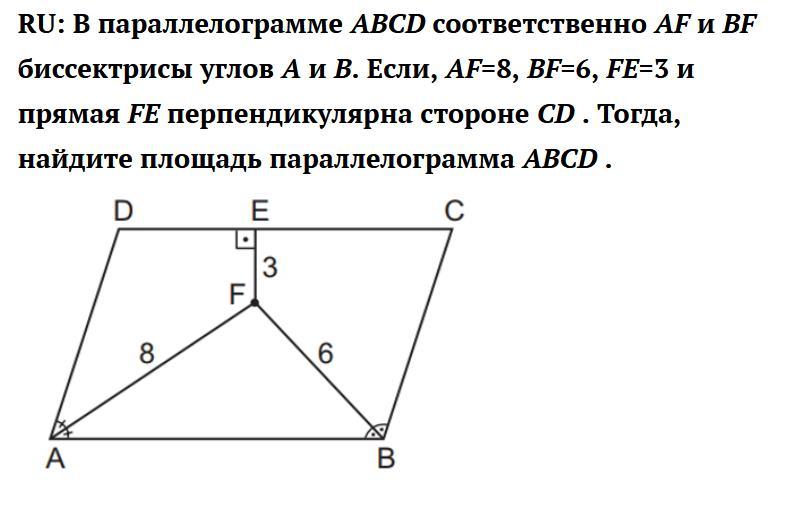
ABCD - пар-м, AF и BF - бис-сы ∠A и ∠B соот-но, AF = 8, BF = 6, FE = 3, FE ⊥ CD

Найти:

S пар-ма

Решение:

Рассмотрим пар-м ABCD: Биссектрисы двух соседних углов параллелограмма всегда образуют угол в 90 градусов, значит ∠AFB = 90°

Продлим прямую EF к стороне AB, т.к EF ⊥ CD, а CD║AB, то EH ⊥ AB

Рассмотрим треугольник AFB: т.к ∠AFB = 90°, то ΔAFB - прямоугольный

Найдем гипотенузу AB по теор.Пифагора:
AB² = AF² + FB²
AB² = 8² + 6² = 64 + 36 = 100
AB = 10

Найдем площадь треугольника по формуле
S = 1/2 ah , где a - основание, h - высота. Представим высоту как катет AF, а основание как катет BF (перемена не сыграет роли), тогда

S = 1/2 * 8 * 6 = 24

Теперь найдем высоту, но обозначив ее как FH, а основание как AB.

h = 2S / a        
h = 2 * 24 / 10 = 4,8

Найдем общую высоту пар-ма, образуемую прямыми EF и FH:
EH = EF + FH = 3 + 4,8 = 7,8

Найдем площадь пар-ма по формуле:
S = ah, где a - основание, h - высота. a = AB, h = EH

S пар-ма = 10 * 7,8 = 78