Предмет: Геометрия,
автор: BlackPhoenixSS
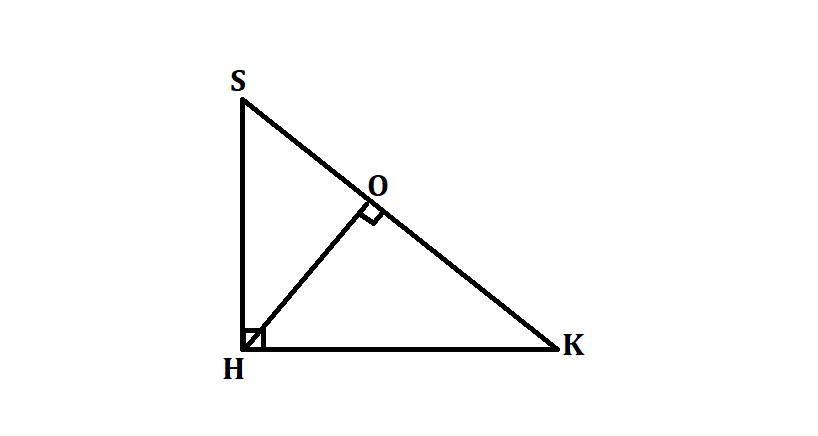
Высота, проведенная из прямого угла треугольника SHK , равна 27 . Найди гипотенузу треугольника SHK , если один из его катетов равен 45.
Ответы
Автор ответа:
7
Ответ:
56,25
Объяснение:
Пусть ∠H = 90°, тогда SK - гипотенуза ΔSHK
HO = 27 - высота
HK = 45
Найдём OK по теореме Пифагора:
- Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: рамиль310
Предмет: Русский язык,
автор: cristinacheh
Предмет: Українська мова,
автор: мінйоншиха77
Предмет: История,
автор: polinnka75
Предмет: География,
автор: supkekcik10202005