Предмет: Алгебра,
автор: m1keyoto
Подати у вигляді суми
Приложения:
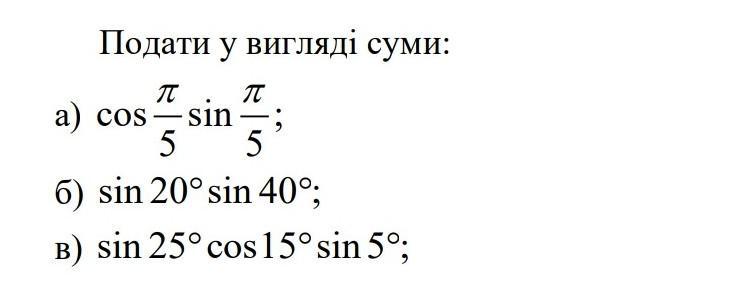
Ответы
Автор ответа:
1
Ответ:
Приложения:
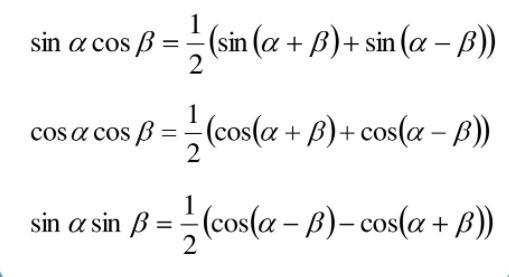
Похожие вопросы
Предмет: Окружающий мир,
автор: Baligas
Предмет: Английский язык,
автор: dementevam2008
Предмет: Русский язык,
автор: rtyuie
Предмет: Қазақ тiлi,
автор: katya200136