Question

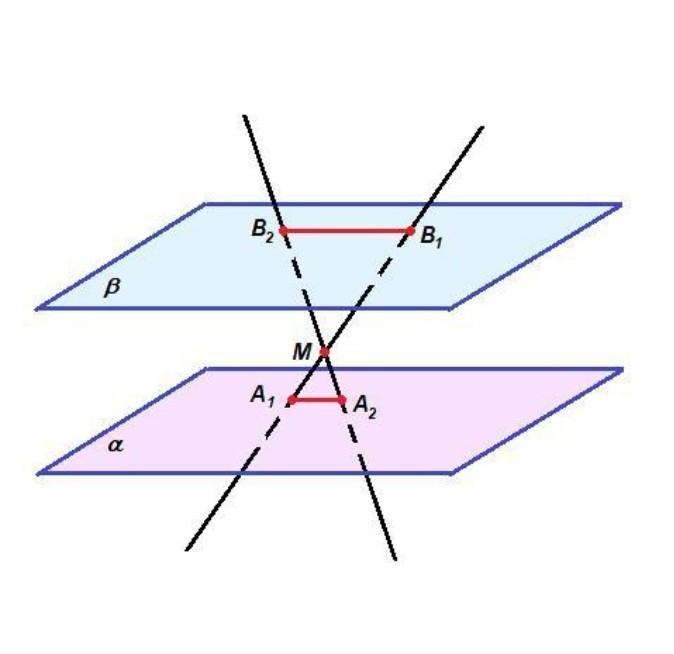
Через точку М проведено дві прямі а і b, що перетинають дві паралельні площини α і β (див. мал.). Першу в точках А1 і А2, другу в точках В1 і В2. Обчисліть МА1 і МВ2, якщо А1А2 : В1В2 = 3 : 4, А1В1= 3,5см, МА2 = 1,2см
допоможіть будь ласка​

Answer 1

Ответ:

Пересекающиеся прямые А₁В₁ и А₂В₂ задают плоскость, которая пересекает плоскости α и β по прямым А₁А₂ и В₁В₂, значит

А₁А₂ ║ В₁В₂.

Тогда ∠МВ₁В₂ = ∠МА₁А₂ как накрест лежащие при пересечении параллельных прямых А₁А₂ и В₁В₂ секущей А₁В₁,

∠В₁МВ₂ = ∠А₁МА₂ как вертикальные, значит

ΔВ₁МВ₂ подобен ΔА₁МА₂ по двум углам.

МВ₂ = А₂В₂ - МА₂ = 10 - 4 = 6 см

\dfrac{A_{1}A_{2}}{B_{1}B_{2}}=\dfrac{MA_{2}}{MB_{2}}

B

1

B

2

A

1

A2

=

MB

2

MA

2

Пусть А₁А₂ = х, тогда В₁В₂ = х + 1,

\dfrac{x}{x+1}=\dfrac{4}{6}

x+1

x

=

6

4

6x = 4(x + 1)

6x = 4x + 4

2x = 4

x = 2

А₁А₂ = 2 см