Предмет: Алгебра,
автор: gjbdtjdsf
7 клас, всё что на фото помогите
Приложения:
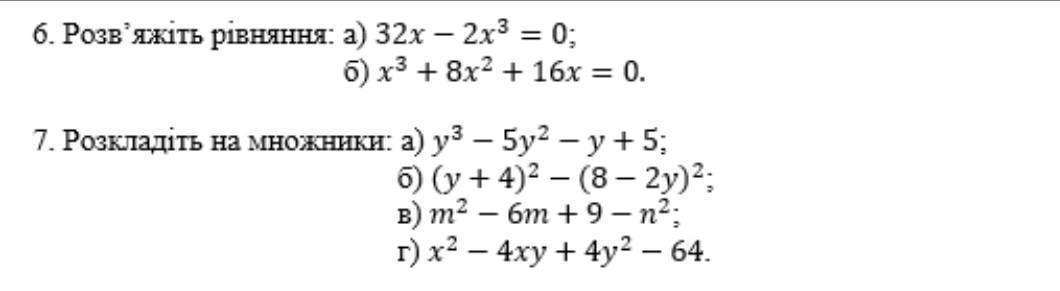
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
1
Ответ: во вложении
Объяснение: в фигурных скобках - черновик - подсказка.
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: romsan12
Предмет: Английский язык,
автор: максим4971
Предмет: Русский язык,
автор: zeynows
Предмет: Математика,
автор: NatsliN87
Предмет: Алгебра,
автор: maxxxssss7