Question

постройте график функции y=-49x+7/7x²-x , и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.

если ответ не правильный , то баллов не будет (вам). даю 100 баллов​

Answer 1

· Преобразуем:

$\sf \displaystyle y=\frac{-49x+7}{7x^2-x}=\frac{-7(7x-1)}{x(7x-1)}=-\frac{7}{x}; \ \ \ \ \ 7x-1 \neq 0 \ \ \Rightarrow \ \ x \neq \frac{1}{7}}$

Функция разрывна в точках x = 0 (бесконечный разрыв), x = 1/7 (выколотая точка).

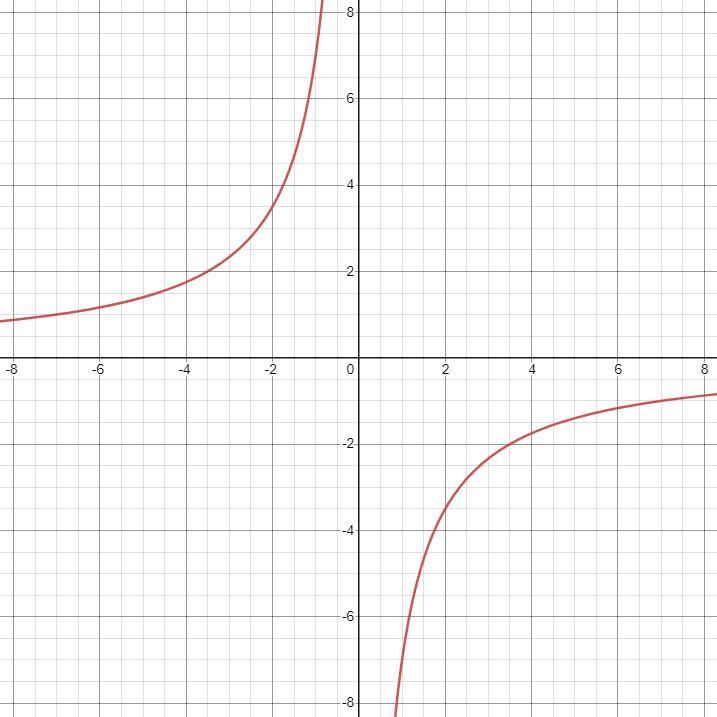
· Графиком функции является гипербола. Таблица точек для построения:

$\sf \displaystyle x: \ \ -7 \ \ -4 \ \ \ \ -1 \ \ \ \ \ 1 \ \ \ \ \ \ \ \ 4 \ \ \ \ \ \ \ 7 \\ y: \ \ \ 1 \ \ \ \ 1.75 \ \ \ \ \ 7 \ \ \ \ -7 \ \ -1.75 \ \ \ -1$

Готовый график смотреть на первой картинке.

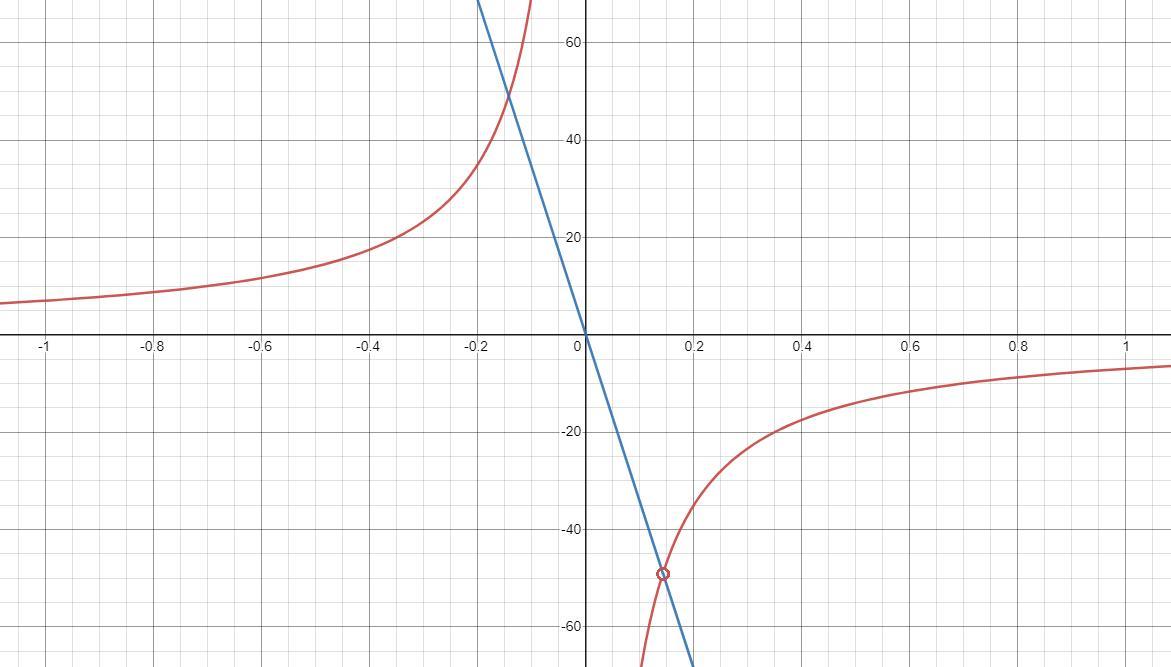
· Прямая y = kx есть прямая, проходящая через начало координат. Коэффициент k задает ее угол наклона. Чтобы прямая пересекла график только в одной точке, пустим ее через найденную ранее выколотую точку (см. вторую картинку).

$\sf \displaystyle x=\frac{1}{7} \ \ \Rightarrow \ \ y=\frac{-7}{\frac{1}{7}}=-49$

- это координаты выколотой точки. Подставим в уравнение:

$\sf \displaystyle -49=\frac{k}{7} \ \ \Rightarrow \ \ \boxed{\sf k=-343}$

Других случаев с одним пересечением нет: при k ∈ [0, +∞) пересечения отсутствуют, при k ∈ (-∞, -343) ∪ (-343, 0) пересечения два.

Ответ:  k = -343