Question

задание на фото, даю 95 балов

Answer 1

$\sf \displaystyle \\ 4|4x+5y-2| \leq 3-2 \sqrt{3x+4y-3}$

Перепишем в виде

$\sf \diaplaystyle 4|4x+5y-2|+2 \sqrt{3x+4y-3} \leq 3$

Заметим, что в левой части находится сумма неотрицательных функций. Отсюда следует, что

$\sf \displaystyle \left \{ {{4|4x+5y-2|\leq 3} \atop {2\sqrt{3x+4y-3}\leq 3}}} \right \ \ \Leftrightarrow \ \ \left \{ {{|4x+5y-2|\leq \frac{3}{4}} \atop {\sqrt{3x+4y-3}\leq \frac{3}{2}}}} \right \ \ \Leftrightarrow \ \ \left \{ {{-\frac{3}{4}\leq4x+5y-2\leq \frac{3}{4}} \atop {0\leq3x+4y-3}\leq \frac{9}{4}}}} \right \\ \\ \Leftrightarrow \left \{ {{\frac{5-16x}{20}\leq y \leq \frac{11-16x}{20}} \atop {\frac{3-3x}{4}}\leq y \leq \frac{21-12x}{16}} \right$

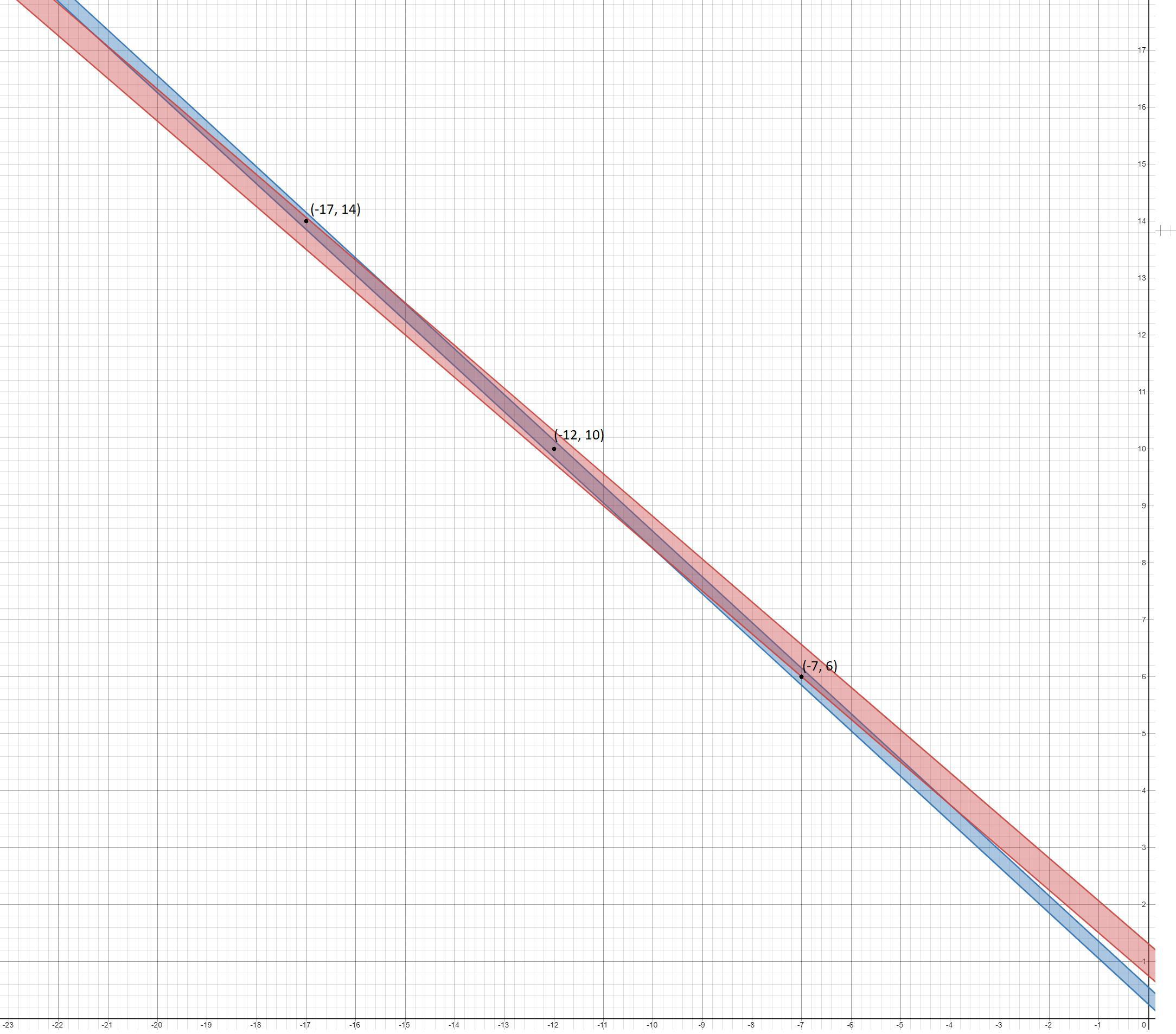
Для этого ослабленного условия построим график (см. картинку). Синяя полоска - первое двойное неравенство, Красная полоска - второе двойное неравенство. Ищем в пересечении полосок точки с целыми координатами (x, y). Таких точек 3: (-7, 6), (-12, 10), (-17, 14). Выберем точку с наибольшим x + y. Это точка (-7, 6). Она удовлетворяет исходному неравенству (это точка пересечения прямых 4x + 5y - 2 = 0 и 3x + 4y - 3 = 0). Таким образом, получен ответ: -7 + 6 = -1.

Ответ: -1