Question

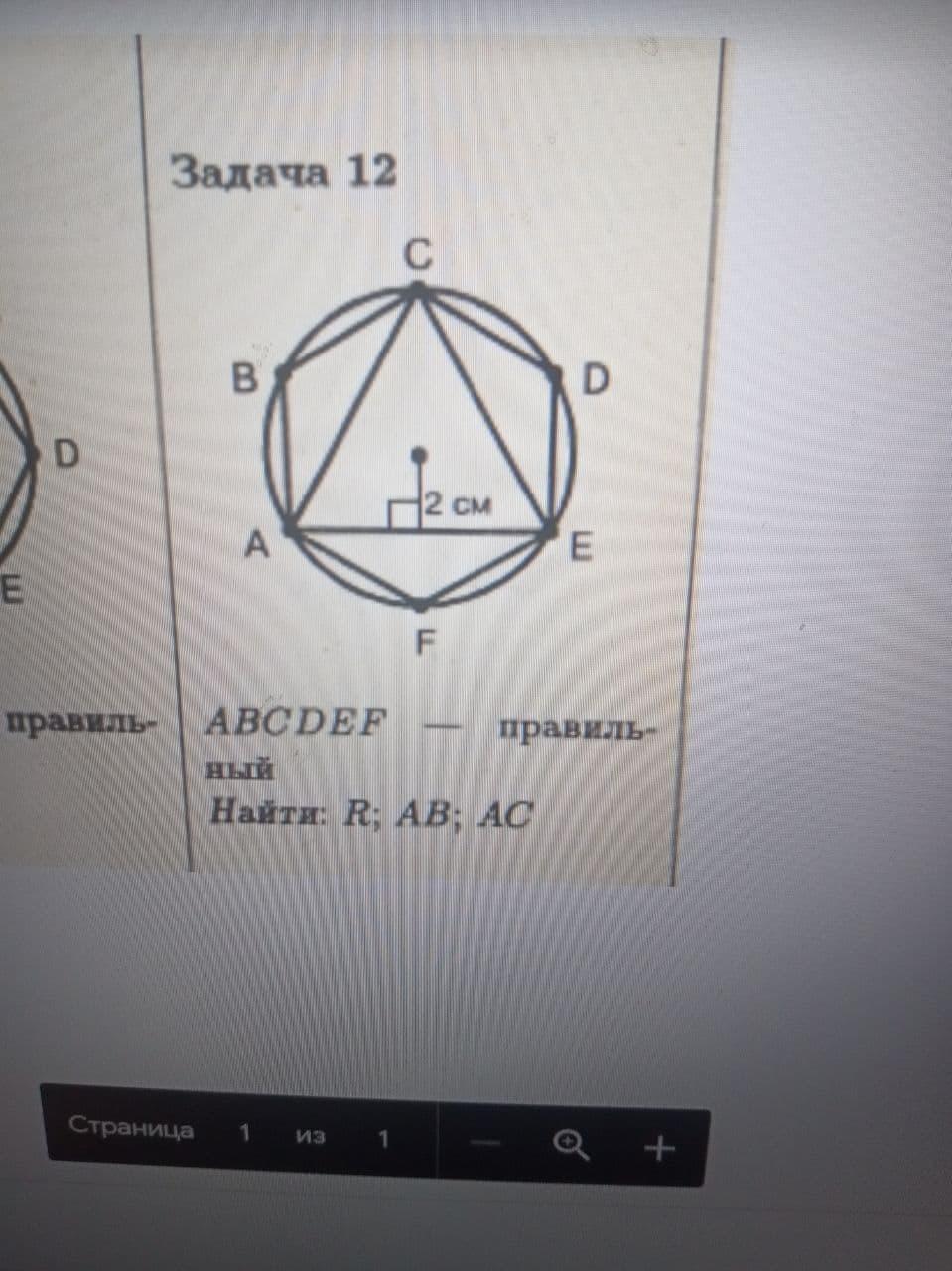
Задача 12
Как найти Радиус описанной окружности шестиугольника? В упор не понимаю

Answer 1

Ответ:R=4; АВ=4; АС=4√3  ;

Объяснение:

Радиус вписанной в равносторонний треугольника АСЕ окружности равен r=R*cos180°/3⇒R=2r=4, радиус описанной около треугольника окружности является и радиусом, описанной около правильного шестиугольника окружности и он равен стороне шестиугольника, т.е. АВ=R=4 сторону треугольника легко посчитать по формуле a₃=R√3=4√3, АС=4√0; можно и без формулы,  а по следствию из теоремы синусов, т.е. АС/sin60°=2R⇒АC=

2*4*√3/2=4√3