Предмет: Алгебра,
автор: friend2013
помогите пожалуйста, заранее спасибо)
Приложения:
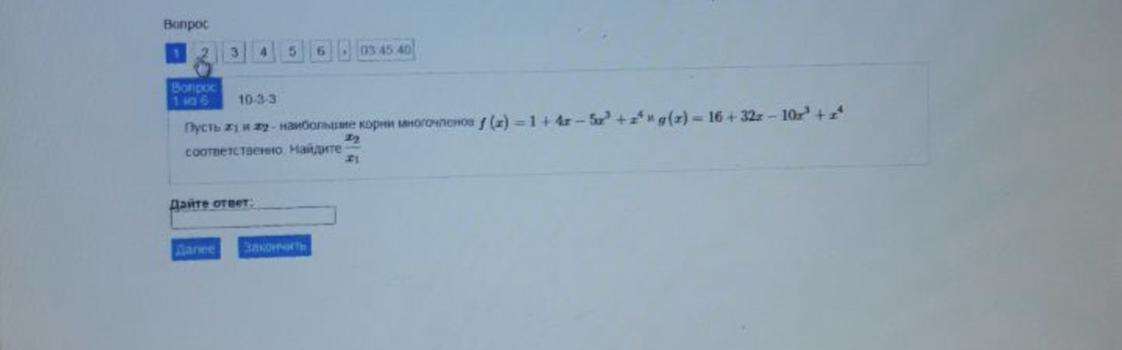
Ответы
Автор ответа:
1
Ответ:
Корни производных этих функций будут относится также, как корни данных функций.
Возмем вторую производную от обеих функций:
f''(x) = 12x² - 15; 12x² = 15; Больший корень
g''(x) = 12x² - 30; 12x² = 30; Больший корень
=>
Объяснение:
Док-во первого утверждения:
Допустим две функции f(x) = (x-x1)(x-x2) = x2 - (x1+x2)x - x1x2;
g(x) = (x-x3)(x-x4) = x2 - (x3+x4)x - x3x4;
И все корни буду относиться как x4 : x2 = x3 : x1 = n (тоесть x4 = n*x2; x3 = n*x1), тогда:
Производные этих функций:
Корни производных функций:
И тогда их отношение -
В решении применил свойство в обратную сторону.
P.S Это конечно частый случай, но свойство рабочее, если очень хочешь могу доказать в общем виде
friend2013:
спасибо
Похожие вопросы
Предмет: Другие предметы,
автор: supievsamir
Предмет: Русский язык,
автор: keryt
Предмет: Русский язык,
автор: Pashka300
Предмет: Русский язык,
автор: adil6417