Предмет: Математика,
автор: vlad1032007
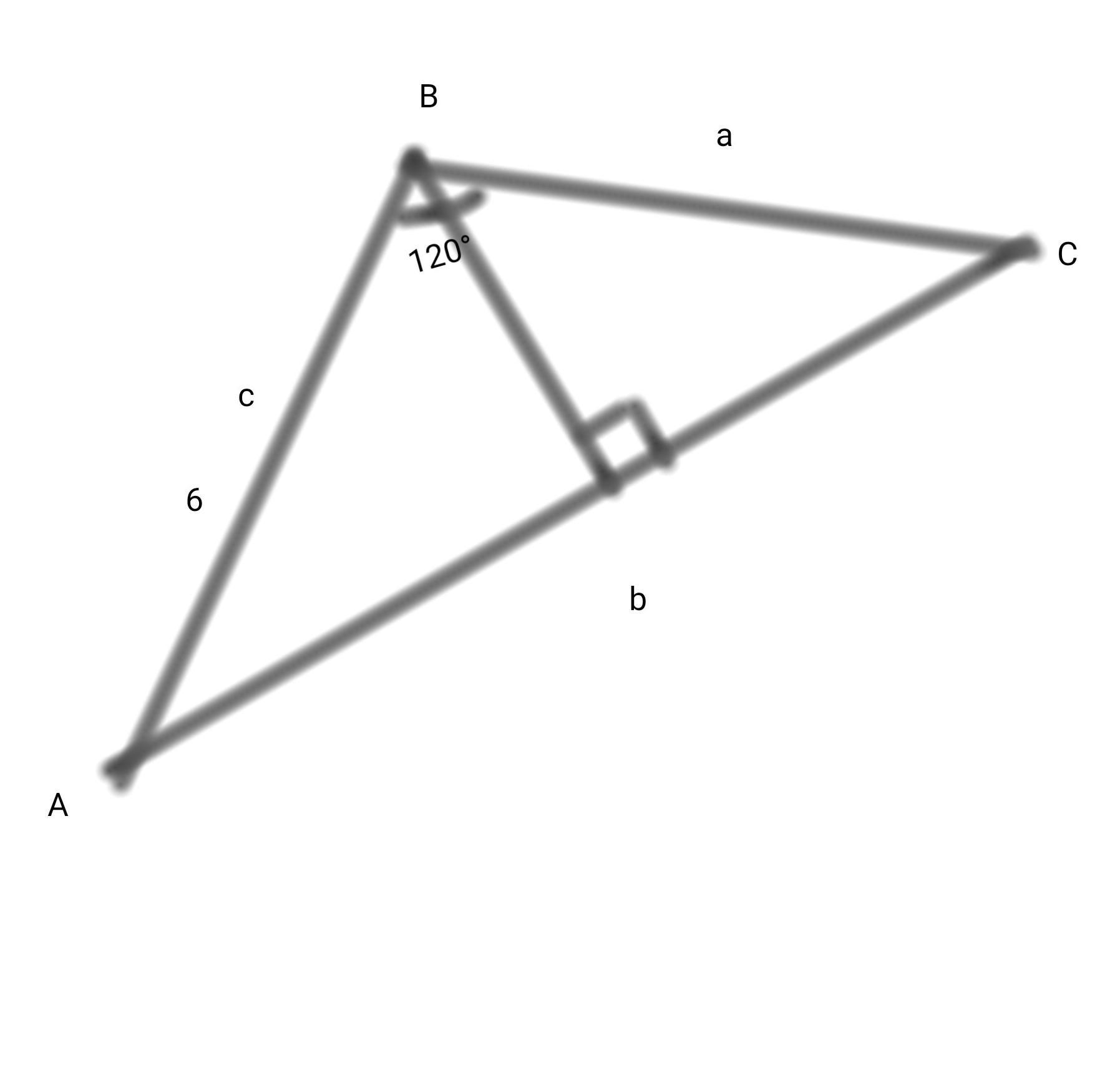
В трикутнику ABC кут ABC=120° AB = 6 см площа трикутника дорівнює 6 корінь з 3 см квадратних ;Обчисліть висоту трикутника проведену до вершини кута B
Ответы
Автор ответа:
1
Ответ:
Площадь треугольника находится по формуле:
Формула высоты из угла ABC
Нам надо найти сторону b=AC.
По теореме косинусов
AC²=AB²+BC²-2×AB×BC×cosB
Теперь найдем высоту
Приложения:
vlad1032007:
спасибо большое
Всегда пожалуйста
Похожие вопросы
Предмет: Английский язык,
автор: tcema
Предмет: Қазақ тiлi,
автор: Fariva
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: aleksangra900