Question

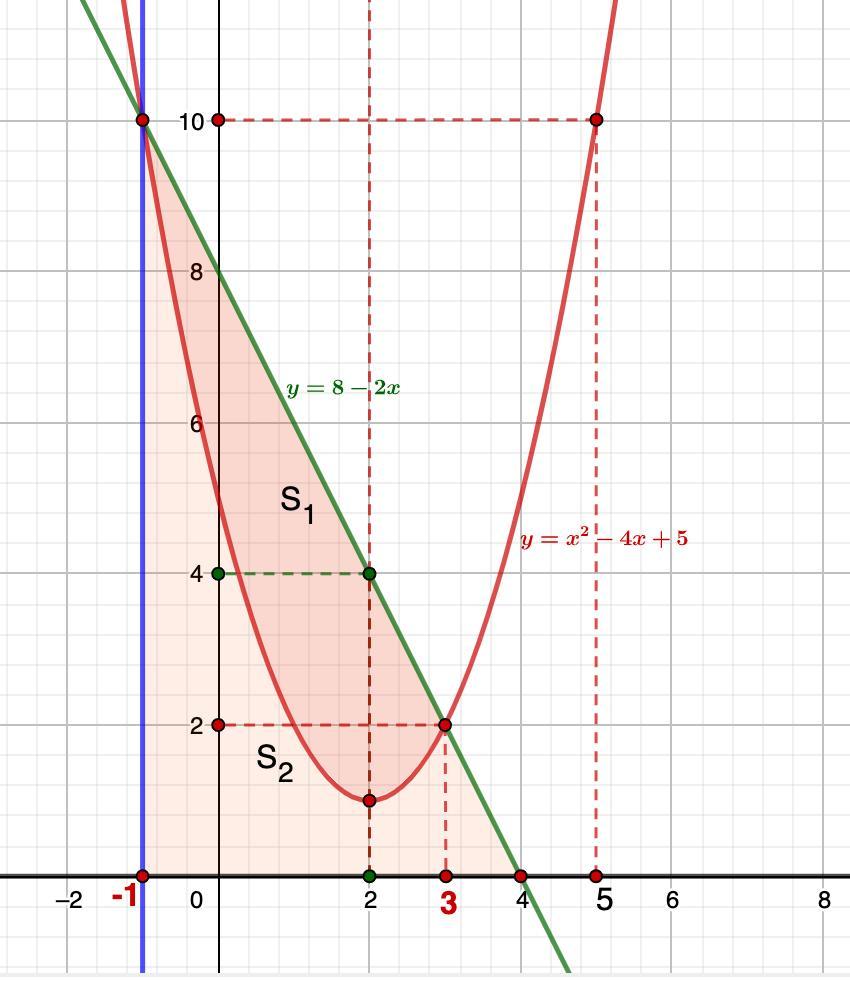
Построй фигуру, ограниченную линиями y=8-2x, y=0, x=-1. График функции y = x^2-4x+5 делит фигуру на две части, найти площадь каждой части.

Answer 1

Ответ:

Площади двух частей фигуры:  $\displaystyle 10\frac{2}{3}\;\;\;u\;\;\;14\frac{1}{3}$

Объяснение:

Требуется построить фигуру, ограниченную линиями y=8-2x, y=0, x=-1. График функции y = x^2-4x+5 делит фигуру на две части, найти площадь каждой части.

Построим графики данных функций и определим фигуру, ограниченную этими графиками.

1. у = 0

Это ось 0х.

2. х = -1

- прямая, проходящая через точку х = -1 и параллельная оси 0у.

3. у = 8 - 2х

- линейная функция, график прямая.

Для построения достаточно двух точек.

х = 2; у = 4

х = -1; у = 10

Получили треугольник, ограниченный тремя линиями.

4. у = х² - 4х + 5

- квадратичная функция, график парабола, ветви вверх.

Вершина:

$\displaystyle x_0=-\frac{b}{2a}=-\frac{-4}{2}=2\\ \\ y_0=2^2-4\cdot 2+5=1$

х₀ = 2 - ось симметрии.

Возьмем еще две точки:

х = 3; у = 2;

х = 5; у = 10

Вторую ветвь построим симметрично прямой х = 2.

5. Найдем точки пересечения графиков  у = х² - 4х + 5 и  у = 8 - 2х:

х² - 4х + 5 = 8 - 2х

х² - 2х -3 = 0

По теореме Виета:

х₁ = -1; х₂ = 3

6. Парабола делит треугольник на две части, площади которых S₁ и S₂.

Найдем площадь треугольника S.

Один катет равен:

4 - (-1) = 5

Другой катет равен 10.

$\displaystyle S = \frac{1}{2}\cdot 5\cdot 10 = 25$  (ед.²)

7. Найдем площадь S₁ по формуле:

$\displaystyle \boxed { S=\int\limits^a_b {(f_2(x)-f_1(x))} \, dx }$

Имеем:

a = 3;  b = -1;  f₂(x) = 8 - 2x;  f₁(x) = x² - 4x + 5

$\displaystyle S_1=\int\limits^3_{-1} {(8-2x-x^2+4x-5)} \, dx =\\\\=\int\limits^3_{-1} {(3+2x-x^2)} \, dx = \left(3x+\frac{2x^2}{2}-\frac{x^3}{3}\right) \;\bigg|^3_{-1} =\\\\=9+9-9-\left(-3+1+\frac{1}{3}\right)=9+1\frac{2}{3} =10\frac{2}{3}$(ед.²)

8. Найдем площадь S₂:

$\displaystyle S_2 = S-S_1=25-10\frac{2}{3}=14\frac{1}{3}$   (ед.²)

Площади частей фигуры  $\displaystyle 10\frac{2}{3}\;\;\;u\;\;\;14\frac{1}{3}$