Предмет: Математика,
автор: Keffon
Вычислите интегралы:
Приложения:
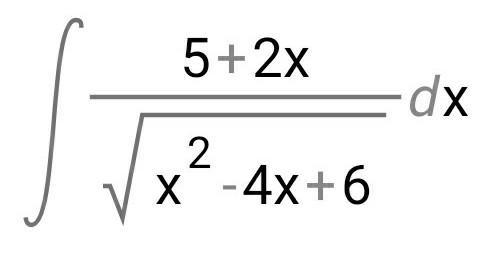
Ответы
Автор ответа:
1
Ответ: 2*√(x²-4*x+6)+ln/x-2+√(x²-4*x+6)/+C
Пошаговое объяснение:
Обозначим интеграл через I(x) и запишем его в виде ∫(2*x-4+9)*dx/√(x²-4*x+6)=∫(2*x-4)*dx/√(x²-4*x+6)+9*∫dx/√(x²-4*x+6)=∫d(x²-4*x+6)/√(x²-4*x+6)+9*∫dx/√(x²-4*x+6)=2*√(x²-4*x+6)+9*∫dx/√(x²-4*x+6). Так как x²-4*x+6=(x-2)²+2=(x-2)²+(√2)², то I(x)=2*√(x²-4*x+6)+9*∫dx/√[(x-2)²+(√2)²]=2*√(x²-4*x+6)+9*∫d(x-2)/√[(x-2)²+(√2)²]. А так как ∫d(x-2)/√[(x-2)²+(√2)²]=ln/x-2+√[(x-2)²+(√2)²]/=ln/x-2+√(x²-4*x+6)/, то I(x)=2*√(x²-4*x+6)+ln/x-2+√(x²-4*x+6)/+C, где C - произвольная постоянная.
Похожие вопросы
Предмет: Английский язык,
автор: tuvspb
Предмет: Окружающий мир,
автор: najabat23
Предмет: Другие предметы,
автор: эля554
Предмет: Английский язык,
автор: solnsevvgb10
Предмет: Английский язык,
автор: АйбаршаХаным