Предмет: Геометрия,
автор: Mickei
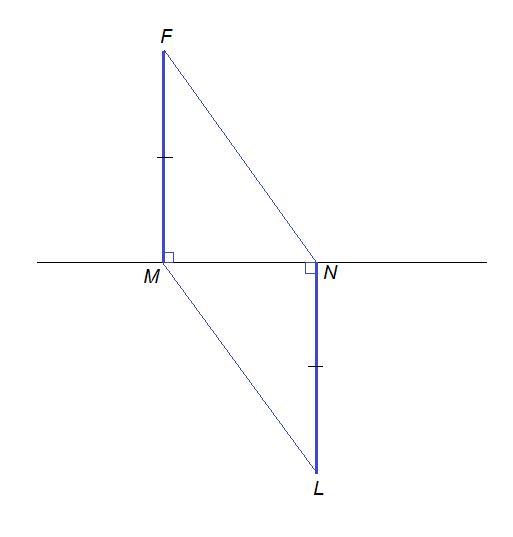
Иs точек F и L, которые расположены по разные стороны от прямой MN,
проведены перпендикуляры FM и LN. Докажи, что Треугольник FMN = Треугольник LNM,
если FM || LN и FM = LN.
Ответы
Автор ответа:
2
Ответ:
ΔFMN = ΔLNM по двум сторонам и углу между ними.
Объяснение:
Если FM║LN, то перпендикуляры FM и LN лежат в одной плоскости.
ΔFMN = ΔLNM по двум сторонам и углу между ними, так как у них:
- ∠FMN = ∠LNM = 90°, так как FM⊥MN, LN⊥MN,
- FM = LN по условию,
- MN - общая сторона.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Susana14
Предмет: Русский язык,
автор: Руфа11
Предмет: Русский язык,
автор: 89090937394
Предмет: География,
автор: sannastia56
Предмет: Русский язык,
автор: 09112012kthfcjrjk