Предмет: Алгебра,
автор: yankemerov1703
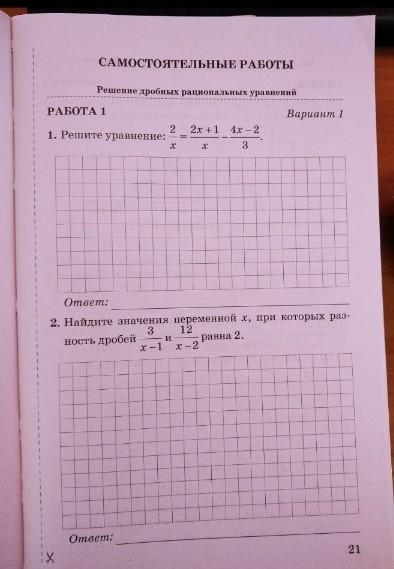
ПОМОГИТЕ ОЧ СРОЧНО. ЗАДАНИЕ В ЗАКРЕПЕ!!!
Приложения:
Ответы
Автор ответа:
1
Объяснение:
1).
2).
yankemerov1703:
СПАСИБО БОЛЬШОЕ, ДАЙ БОГ ВАМ ЗДОРОВЬЯ!
Похожие вопросы
Предмет: Английский язык,
автор: makkotow
Предмет: Русский язык,
автор: badalovaanzhel
Предмет: Русский язык,
автор: imalysheva042
Предмет: Русский язык,
автор: ilyaleyman
Предмет: Другие предметы,
автор: oksansotdelnova