Предмет: Математика,
автор: bogomolovan882
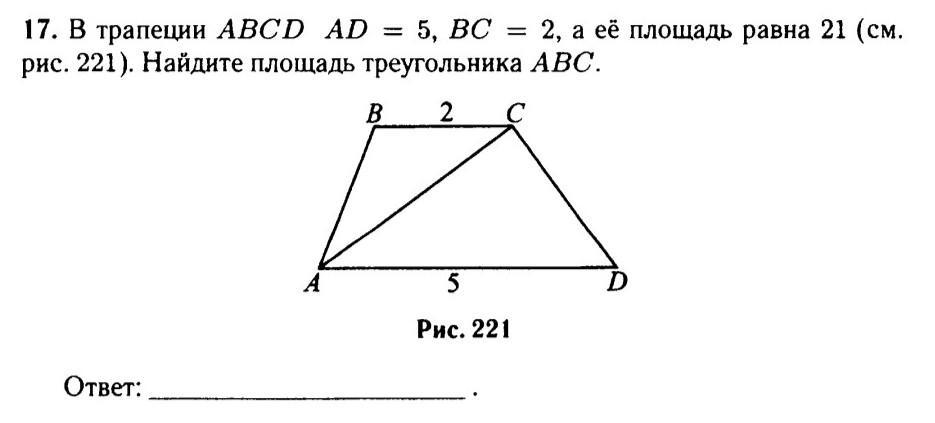
В трапеции ABCD AD=5, BC=2, а её площадь равна 21 (см. рис. 221). Найдите площадь треугольника ABC
СРОЧНО
Приложения:
Ответы
Автор ответа:
6
Ответ:
Площадь треугольника Δ АВС равна 6 кв. ед.
Пошаговое объяснение:
Дана трапеция АВСD
Площадь трапеции равна 21. Площадь трапеции определяется по формуле
где
a,b- основания трапеции
h- высота трапеции.
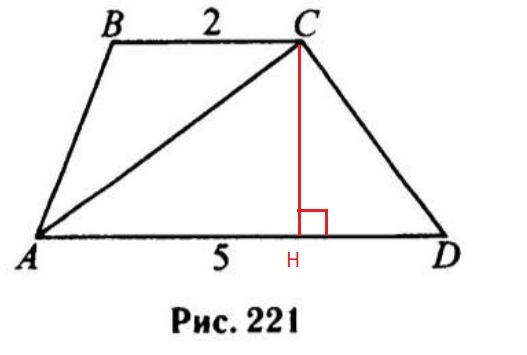
Проведем высоту трапеции СН и зная площадь и основания, найдем высоту
Значит, высота СН =6 .
Эта высота является высотой треугольника Δ АСD.
Найдем площадь данного треугольника как полупроизведение стороны на высоту, проведенную к данной высоте.
Площадь треугольника Δ АВС равна разности площади трапеции и площади Δ АСD.
Тогда площадь треугольника Δ АВС
Площадь треугольника Δ АВС равна 6 кв. ед.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Айгулька09082006
Предмет: Английский язык,
автор: probrabus
Предмет: Английский язык,
автор: Sad911
Предмет: Русский язык,
автор: аааа315
Предмет: Математика,
автор: Monya1231