Предмет: Алгебра,
автор: fhntv445
Знайдіть найбільший кут трикутника, якщо його сторони дорівнюють 3 см, 5 см і 7 см
Ответы
Автор ответа:
3
Ответ:
наибольший угол равен 120°.
Объяснение:
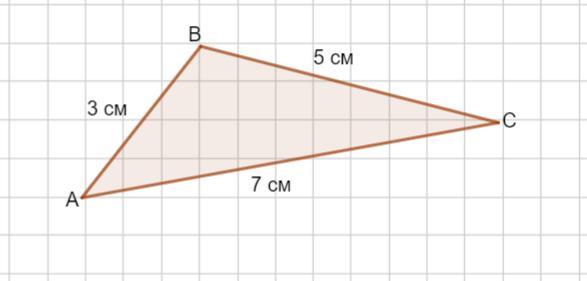
Пусть дан треугольник Δ АВС . АВ= 3см, ВС= 5 см, АС= 7 см .
Наибольший угол лежит напротив наибольшей стороны.
Так как сторона АС наибольшая , то ∠ В - наибольший.
Применим теорему косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
∠B = 120°
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Другие предметы,
автор: mirkasimov06
Предмет: Русский язык,
автор: malyhinvalik
Предмет: Химия,
автор: mrmishaak47