Очень срочно нужна помощь в решении задания по алгебре.

Ответы
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!!!
Ответ:
Изобразили графически решение системы неравенств.
Объяснение:
Требуется изобразить графически решение системы неравенств.
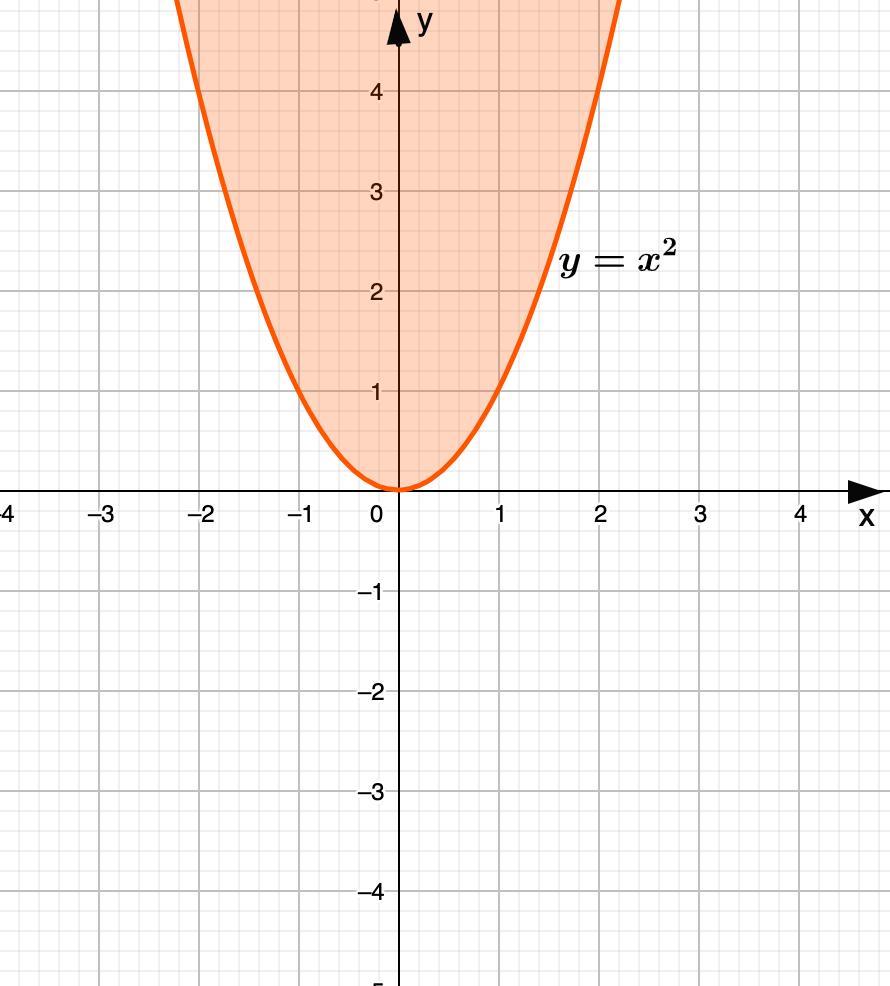
1. Построим график
у = х²
- парабола, ветви вверх (числовой коэффициент при х² положительный).
Вершина в точке (0; 0)
Возьмем несколько точек:
х = ±1; у = 1
х = ±2; у=4
х = ±3; у=9
Построим график.
Решением неравенства
у ≥ х²
будет область выше графика (оранжевая). Так как неравенство нестрогое, то сам график тоже входит в решение.
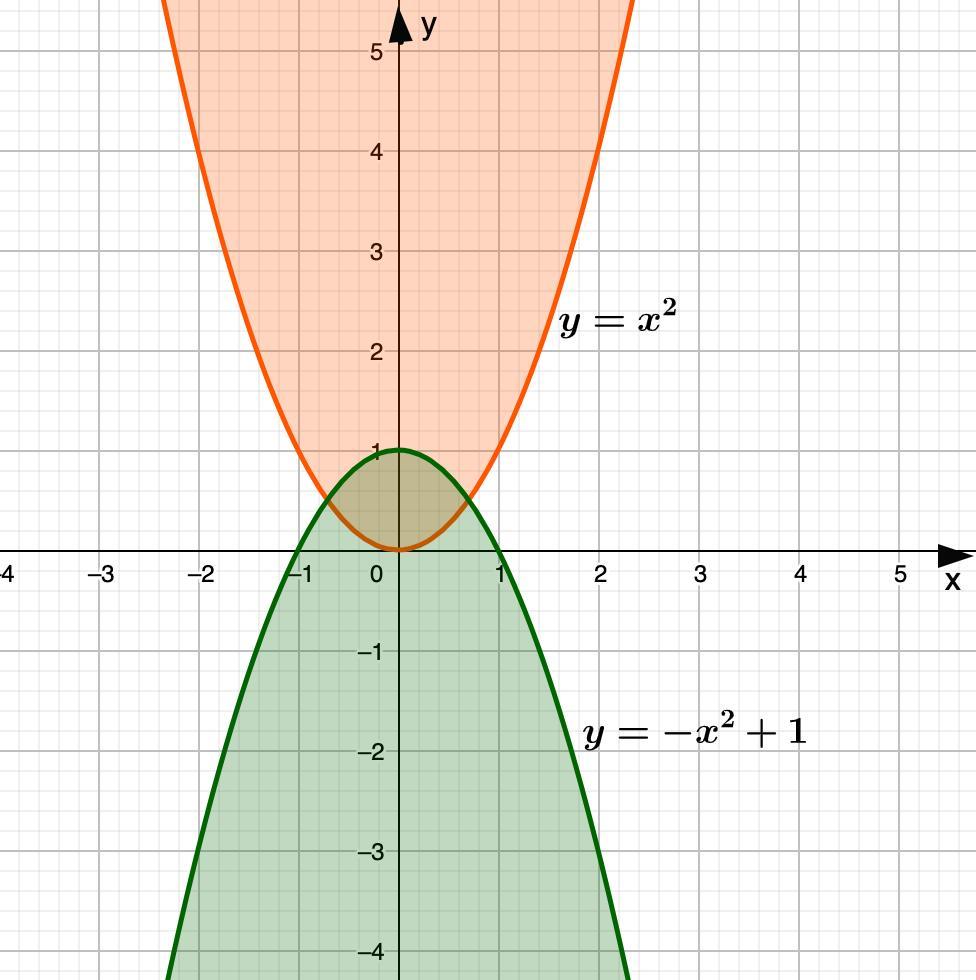
2. Построим график
у = -х² + 1
-парабола, ветви вниз (числовой коэффициент при х² отрицательный)
Этот график получим путем зеркального отображения графика
у = х²
относительно оси 0х и сдвигом вверх на 1 единицу.
Решением неравенства
у ≤ -х² + 1
будет область ниже графика (зеленая). Неравенство нестрогое, поэтому сам график тоже входит в решение неравенства.
Ну, а решением неравенства будет область пересечения
оранжевой и зеленой областей.