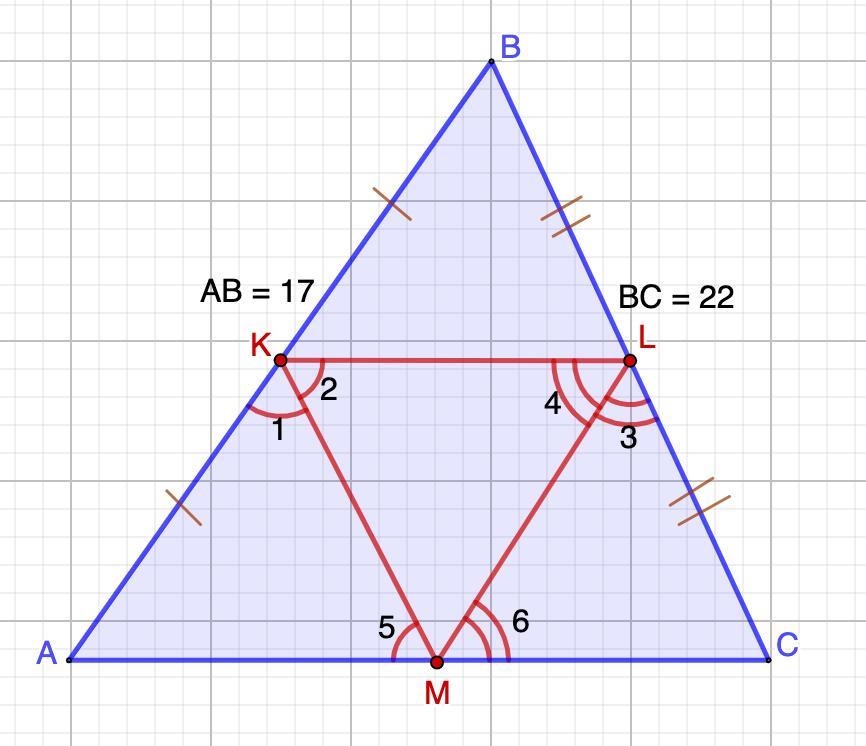
Дан треугольник ABC. Точки K и L — середины сторон AB и BC соответственно. Оказалось, что биссектрисы углов AKL и CLK пересекаются на отрезке AC. Найдите длину отрезка AC, если известно, что AB=17 и BC=22.
Ответы
Ответ:
Длина отрезка АС равна 19,5 ед.
Пошаговое объяснение:
Требуется найти длину отрезка АС.
Дано: ΔАВС;
АК = КВ; BL = LC;
К ∈ АВ; L ∈ BC;
KM - биссектриса ∠AKL;
LM - биссектриса ∠CLK;
КМ ∩ LM = M; M ∈ AC;
AB = 17; BC = 22.
Найти: АС.
Решение:
Пусть угол АКМ равен углу 1, угол МКL равен углу 2, угол MLC равен углу 3, угол KLM равен углу 4, угол АМК равен углу 5, угол LMC углу 6.
1. Рассмотрим ΔАВС.
АК = КВ; BL = LC (условие)
- Отрезок, соединяющий середины двух сторон треугольника называется средней линией треугольника.
⇒ КL - средняя линия ΔАВС (по определению)
Средняя линия треугольника соединяет середины двух его сторон и параллельна третьей стороне.
⇒ KL || AC
2. Рассмотрим ΔАКМ
∠1 = ∠2 (KM - биссектриса ∠AKL)
∠5 = ∠2 (накрест лежащие при KL || AC и секущей КМ)
⇒ ∠1 = ∠5
- Если в треугольнике два угла равны, то этот треугольник - равнобедренный.
⇒ ΔАКМ - равнобедренный.
АМ = АК.
АМ = АК = КВ = АВ : 2 = 17 : 2 = 8,5 (ед.)
3. Рассмотрим ΔMLC.
∠3 = ∠4 (LM - биссектриса ∠CLK)
∠6 = ∠4 (накрест лежащие при KL || AC и секущей LМ)
⇒ ∠3 = ∠6.
ΔMLC - равнобедренный.
MC = CL.
MC = CL = LB = BC : 2 = 22 : 2 = 11 (ед.)
4. АС = АМ + MC = 8,5 + 11 = 19,5 (ед.)
Отрезок АС равен 19,5 ед.