Question

Докажите, что если один из углов прямоугольного треугольника равен 30°, то катет, лежащий против этого угла, равен половине гипотенузы​

Answer 1

Объяснение:

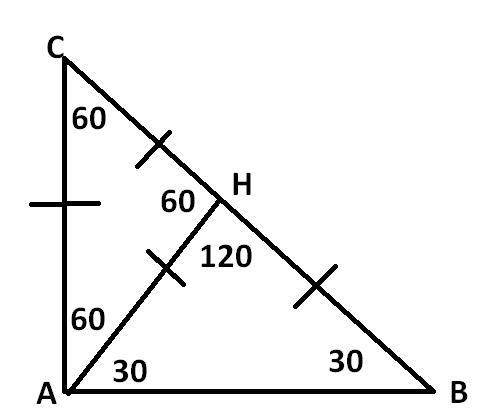
Пусть в прямоугольном треугольнике АВС угол B=30°, угол A=90°; ∠C=90-30=60°

Проведем из прямого угла отрезок AH так, что угол CAH=60°; ∠CHA=180-60-60=60°;
ΔCAH равносторонний⇒CH=AC;
∠AHB=180-60=120°; ∠BAH=180-120-30=30°
ΔAHB равнобедренный; значит AH=HB;
Имеем AC=AH=CH=HB;
AB=CH+HB=AC+AC=2AC;
AC=1/2AB;
AB-гипотенуза; AC-катет против угла в 30°
Что и требовалось доказать