Предмет: Математика,
автор: versachexdior
Упростите выражение и найдите его числовое значение
решите 3) и 4)
Приложения:
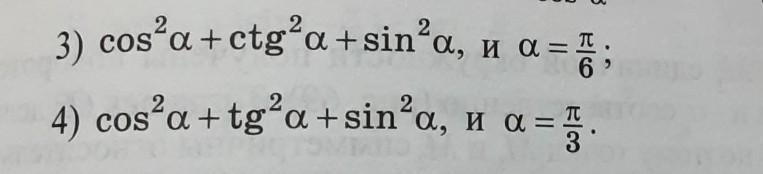
gulicham16:
qaysi misol bu
267
hoz
Ответы
Автор ответа:
1
Пошаговое объяснение:
3) Упростим выражение
При
4) Упростим выражение
При
Спасибо большое❤
Автор ответа:
1
Ответ: 3) 4
4) 4
Пошаговое объяснение:
3. (cos²α+sin²α)+ctg²α=1+ctg²β=1/sin²α; 1/sin²π/6=1/(1/2)²=4
4)(cos²α+sin²α)+tg²α=1+tg²β=1/cos²α; 1cos²π/3=1/(1/2)²=4
использовала основные тригонометрические тождества
(cos²α+sin²α)=1; 1+ctg²β=1/sin²α; 1+tg²β=1/cos²α
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Jes1930
Предмет: Русский язык,
автор: vladasaru28
Предмет: Литература,
автор: nik4330