Предмет: Математика,
автор: CasseGig
вычислите пожалуйста подробно определенный интеграл
Приложения:

Ответы
Автор ответа:
0
Приложения:

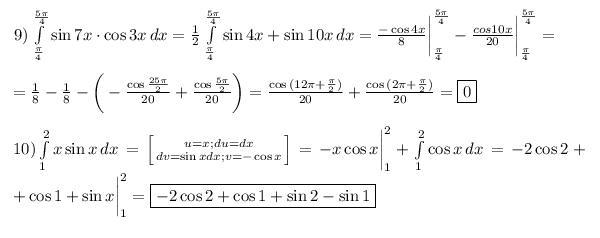
Похожие вопросы
Предмет: Русский язык,
автор: odloko
Предмет: Русский язык,
автор: milekhina81
Предмет: Русский язык,
автор: Анна20223
Предмет: Геометрия,
автор: LinaMakLagenn
Предмет: Математика,
автор: Покрасьон